Question

11．在四棱锥P-ABCD中，∠ABC=∠ACD=90°，∠BAC=∠CAD=60°，PA⊥平面ABCD，E为PD的中点，PA=2AB=2．
（1）求证：CE∥平面PAB．
（2）若F为PC的中点，求F到平面AEC的距离．

Answer 1

分析 （1）取AD中点M，连EM，CM．说明EM∥PA．推出EM∥平面PAB，证明MC∥平面PAB，然后证明EC∥平面PAB．
（2）说明EF为三棱锥E-AFC的高，设F到平面AEC的距离为h，利用V_E-FAC=V_F-AEC，求解F到平面AEC的距离．

解答 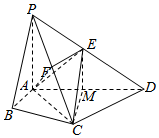（1）证明：在Rt△ABC中，AB=1，∠BAC=60°，∴BC=$\sqrt{3}$，AC=2．
取AD中点M，连EM，CM．则EM∥PA．
∵EM?平面PAB，PA?平面PAB，∴EM∥平面PAB
在Rt△ACD中，∠CAD=60°，AC=AM=2，
∴∠ACM=60°．而∠BAC=60°，∴MC∥AB．
∵MC?平面PAB，AB?平面PAB，∴MC∥平面PAB 
∵EM∩MC=M，∴平面EMC∥平面PAB．
∵EC?平面EMC，∴EC∥平面PAB-----------（5分）
（2）解：∵PA=CA，F为PC的中点，∴AF⊥PC
∵PA⊥平面ABCD，∴PA⊥CD．
∵AC⊥CD，PA∩AC=A，∴CD⊥平面PAC．
又EF∥CD，∴EF⊥平面PAC．即EF为三棱锥E-AFC的高
因为$CD=2\sqrt{3}$，得$EF=\sqrt{3}$，-----------（7分）
从而${V_{E-FAC}}=\frac{1}{3}×\frac{1}{2}（\frac{1}{2}AC•AP）•EF=\frac{1}{3}×\frac{1}{2}（\frac{1}{2}×2×2）×\sqrt{3}=\frac{{\sqrt{3}}}{3}$
在Rt△PAD中，$AE=CE=\frac{1}{2}PD=\frac{1}{2}×\sqrt{{2^2}+{2^2}+{{（2\sqrt{3}）}^2}}=\sqrt{5}$
于是${S_{△ACE}}=\frac{1}{2}AC•\sqrt{{{（\sqrt{5}）}^2}-1}=2$，设F到平面AEC的距离为h
由V_E-FAC=V_F-AEC即$\frac{1}{3}×2h=\frac{{\sqrt{3}}}{3}⇒h=\frac{{\sqrt{3}}}{2}$
故F到平面AEC的距离为$\frac{{\sqrt{3}}}{2}$------------（12分）

点评 本题考查直线与平面平行，平面与平面平行的判断与性质，点到平面的距离的距离的求法，等体积方法的应用，考查转化思想以及计算能力．