
| A. | $\frac{20}{27}$ | B. | $\frac{8}{27}$ | C. | $\frac{7}{27}$ | D. | $\frac{1}{27}$ |
分析 先根据变量ξ~B(2,p),且P(ξ≥1)=1-P(ξ<1)=$\frac{5}{9}$,求出p的值,然后根据P(η≥2)=1-P(η=0)-P(η=1)求出所求.
解答 解:∵变量ξ~B(2,p),且P(ξ≥1)=$\frac{5}{9}$,
∴P(ξ≥1)=1-P(ξ<1)=1-C20•(1-p)2=$\frac{5}{9}$,
∴p=$\frac{1}{3}$,
∴P(η≥2)=1-P(η=0)-P(η=1)=1-C30( $\frac{1}{3}$)0( $\frac{2}{3}$)3 -${C}_{3}^{1}$•$\frac{1}{3}$•${(\frac{2}{3})}^{2}$=1-$\frac{8}{27}$-$\frac{12}{27}$=$\frac{7}{27}$,
故选:C.
点评 本题主要考查了二项分布与n次独立重复试验的模型,解题的关键就是求p的值,属于中档题.


 优加精卷系列答案
优加精卷系列答案科目:高中数学 来源: 题型:选择题
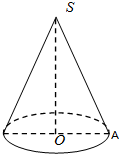 如图,课桌上放着一个圆锥SO,点A为圆锥底面圆周上一点,SA=2cm,OA=1cm,蚂蚁从点A沿圆锥的侧面爬行一周再回到A,则蚂蚁行迹的最短路程是( )
如图,课桌上放着一个圆锥SO,点A为圆锥底面圆周上一点,SA=2cm,OA=1cm,蚂蚁从点A沿圆锥的侧面爬行一周再回到A,则蚂蚁行迹的最短路程是( )| A. | 2πcm | B. | 2$\sqrt{2}$cm | C. | 4$\sqrt{2}$cm | D. | 4cm |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | -$\frac{1}{3}$ | D. | -$\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{AB}{DE}=\frac{AD}{BE}$ | B. | $\frac{BC}{AC}=\frac{EF}{DF}$ | C. | $\frac{AC}{AB}=\frac{DF}{EF}$ | D. | $\frac{AB}{EF}=\frac{DE}{BC}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\left\{{\begin{array}{l}{x=1+\frac{1}{2}t}\\{y=5+\frac{{\sqrt{3}}}{2}t}\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}{x=1+\frac{{\sqrt{3}}}{2}t}\\{y=5+\frac{1}{2}t}\end{array}}\right.$ | C. | $\left\{{\begin{array}{l}{x=1+\frac{{\sqrt{3}}}{2}t}\\{y=5-\frac{1}{2}t}\end{array}}\right.$ | D. | $\left\{{\begin{array}{l}{x=1+\frac{1}{2}t}\\{y=5-\frac{{\sqrt{3}}}{2}t}\end{array}}\right.$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 8 | C. | 16 | D. | 64 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com