
分析 由切线的倾斜角为$\frac{3π}{4}$,算出切线的斜率k=-1.设切点的坐标为(a,a2),求出函数y=x2的导数为y′=2x,根据导数的几何意义得2a=-1,解得a=-$\frac{1}{2}$,从而可得切点的坐标.
解答 解:设切点的坐标为(a,a2)
∵切线的倾斜角为$\frac{3π}{4}$,
∴切线的斜率k=tan$\frac{3π}{4}$=-1.
对y=x2求导数,得y′=2x,
∴2a=-1,得a=-$\frac{1}{2}$,
可得切点的坐标为(-$\frac{1}{2}$,$\frac{1}{4}$).
故答案为:(-$\frac{1}{2}$,$\frac{1}{4}$).
点评 本题求抛物线y=x2上切线的倾斜角为$\frac{3π}{4}$的点的坐标.着重考查了抛物线的性质、导数的几何意义、直线与抛物线的关系等知识,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
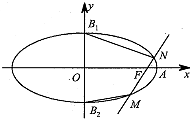 已知椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),其右顶点为 A(2,0),上、下顶点分别为 B1,B2.直线 A B2的斜率为$\frac{1}{2}$,过椭圆的右焦点F的直线交椭圆于 M,N两点( M,N均在y轴右侧).
已知椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),其右顶点为 A(2,0),上、下顶点分别为 B1,B2.直线 A B2的斜率为$\frac{1}{2}$,过椭圆的右焦点F的直线交椭圆于 M,N两点( M,N均在y轴右侧).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,-2) | B. | (-2,1) | C. | (-1,2) | D. | (2,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图是某几何体的三视图(单位:cm),正视图是等腰梯形,俯视图中的曲线是两个同心的半圆,侧视图是直角梯形.则该几何体的体积等于( )
如图是某几何体的三视图(单位:cm),正视图是等腰梯形,俯视图中的曲线是两个同心的半圆,侧视图是直角梯形.则该几何体的体积等于( )| A. | 28 πcm3 | B. | 14πcm3 | C. | 7πcm3 | D. | 56πcm3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
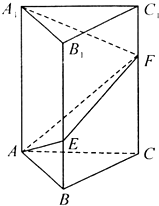 如图,在直三棱柱ABC-A1B1C1中,已知∠BAC=90°,AB=AC=1,AA1=3,点E,F分别在棱BB1,CC1上,且C1F=$\frac{1}{3}$C1C,BE=$\frac{1}{3}$BB1.
如图,在直三棱柱ABC-A1B1C1中,已知∠BAC=90°,AB=AC=1,AA1=3,点E,F分别在棱BB1,CC1上,且C1F=$\frac{1}{3}$C1C,BE=$\frac{1}{3}$BB1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com