
分析 (1)求出圆C圆心,半径为,设M(x,y),则$\overrightarrow{CM}=(x,y-2),\overrightarrow{MP}=(1-x,1-y)$.利用$\overrightarrow{CM}•\overrightarrow{MP}=0$,求出M的轨迹方程.
(2)假设存在点M(x,y),满足OP⊥OM,求出P(1,1),M(x,y),通过$\overrightarrow{OP}•\overrightarrow{OM}=x+y=0$,利用点M的运动轨迹为:${(x-\frac{1}{2})^2}+{(y-\frac{3}{2})^2}=\frac{1}{2}$,将y=-x带入圆的方程,化简得:x2+x+1=0,方程无解,即可得到结果.
解答 解:(1)圆C的方程可化为x2+(y-2)2=4,
所以圆心为C(0,2),半径为2,(2分)
设M(x,y),则$\overrightarrow{CM}=(x,y-2),\overrightarrow{MP}=(1-x,1-y)$.
由题设知$\overrightarrow{CM}•\overrightarrow{MP}=0$,故x(1-x)+(y-2)(1-y)=0,
即${(x-\frac{1}{2})^2}+{(y-\frac{3}{2})^2}=\frac{1}{2}$.(5分)
由于点P在圆C内部,所以M的轨迹方程
是${(x-\frac{1}{2})^2}+{(y-\frac{3}{2})^2}=\frac{1}{2}$.(6分)
(2)假设存在点M(x,y),满足OP⊥OM则 $\overrightarrow{OP}=(1,1),\overrightarrow{OM}=(x,y)$,
若OP⊥OM,P(1,1),M(x,y),$\overrightarrow{OP}•\overrightarrow{OM}=x+y=0$,则y=-x (8分)
又因为点M的运动轨迹为:${(x-\frac{1}{2})^2}+{(y-\frac{3}{2})^2}=\frac{1}{2}$,
所将y=-x带入方程${(x-\frac{1}{2})^2}+{(y-\frac{3}{2})^2}=\frac{1}{2}$ (10分)
化简得:x2+x+1=0 (*)
方程 (*)无解,所以不存在满足OP⊥OM的点M.(12分)
点评 本题考查轨迹方程的求法,直线与圆的方程的综合应用,考查计算能力以及转化思想.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{16}{25}$. | B. | $\frac{9}{16}$ | C. | $\frac{36}{61}$ | D. | $\frac{20}{61}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
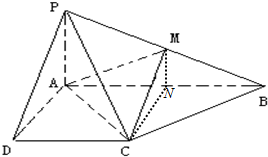 已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=$\frac{1}{2}$,AB=1,M是PB的中点.N是AB的中点.
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=$\frac{1}{2}$,AB=1,M是PB的中点.N是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
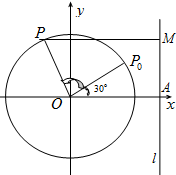 如图,圆O的半径为2,l为圆O外一条直线,圆心O到直线l的距离|OA|=3,P0为圆周上一点,且∠AOP0=$\frac{π}{6}$,点P从P0处开始以2秒一周的速度绕点O在圆周上按逆时针方向作匀速圆周运动.t秒钟后,点P到直线l的距离用t(t≥0)可以表示为3-2cos(πt+$\frac{π}{6}$),t≥0.
如图,圆O的半径为2,l为圆O外一条直线,圆心O到直线l的距离|OA|=3,P0为圆周上一点,且∠AOP0=$\frac{π}{6}$,点P从P0处开始以2秒一周的速度绕点O在圆周上按逆时针方向作匀速圆周运动.t秒钟后,点P到直线l的距离用t(t≥0)可以表示为3-2cos(πt+$\frac{π}{6}$),t≥0.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
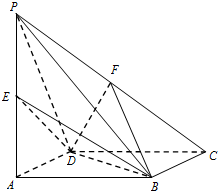 如图,在四棱锥P-ABCD中,底面ABCD是边长为1的菱形,∠BAD=60°,侧棱PA⊥底面ABCD,E、F分别是PA、PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是边长为1的菱形,∠BAD=60°,侧棱PA⊥底面ABCD,E、F分别是PA、PC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com