
分析 (Ⅰ)由题意可知:椭圆C的离心率为e=$\frac{c}{a}$$\frac{{\sqrt{3}}}{2}$,即3a2=4c2,则a2=4b2,设椭圆C的方程为$\frac{y^2}{{4{b^2}}}+\frac{x^2}{b^2}=1$,抛物线x2=8y的准线方程为y=-2,它与y轴的交点(0,-2)是椭圆的一个顶点,a=2,b=1,即可求得椭圆的标准方程;
(Ⅱ)将直线方程代入抛物线方程,由△=64-32b>0,则b<2,x3+x4=8,x3x4=8b,x3+x4=8,x3x4=8b,$\overrightarrow{OM}•\overrightarrow{ON}=0$,则x3y3+x4y4=0,则x3x4+y3y4=0,$⇒2{x_3}{x_4}-b({x_3}+{x_4})+{b^2}=0$,b=0或-8 经检验,符合题意,即可求得实数b的值;
(Ⅲ)设切线l的方程为y=kx+m,代入椭圆方程,则${x_1}+{x_2}=-\frac{2km}{{{k^2}+4}}$,${x_1}{x_2}=\frac{{{m^2}-4}}{{{k^2}+4}}$,又由l与圆x2+y2=1相切,$\frac{|m|}{{\sqrt{{k^2}+1}}}=1$,k2=m2-1,则$|AB|=\sqrt{1+{k^2}}\sqrt{{{({x_1}+{x_2})}^2}-4{x_1}{x_2}}$,即可求得${S_{△AOB}}=\frac{1}{2}|{AB}|=\frac{{2\sqrt{3}|m|}}{{{m^2}+3}}$,|m|≥1,由基本不等式的性质即可求得S△A0B的最大值.
解答 解:(Ⅰ) 椭圆C的离心率为e=$\frac{c}{a}$$\frac{{\sqrt{3}}}{2}$,即3a2=4c2,
由a2=b2+c2,则a2=4b2,
设椭圆C的方程为$\frac{y^2}{{4{b^2}}}+\frac{x^2}{b^2}=1$,…(1分)
抛物线x2=8y的准线方程为y=-2,它与y轴的交点(0,-2)是椭圆的一个顶点,
故a=2,
∴b=1,…(2分)
∴椭圆C的标准方程为$\frac{y^2}{4}+{x^2}=1$,
椭圆C的“伴随”方程为x2+y2=1.…(3分)
(Ⅱ)设M(x3,y3),N(x4,y4),
$\left\{\begin{array}{l}{y=x-b}\\{{x}^{2}=8y}\end{array}\right.$,整理得:x2-8x+8b=0,
△=64-32b>0,
∴b<2
则x3+x4=8,x3x4=8b,
$\overrightarrow{OM}•\overrightarrow{ON}=0$,则x3y3+x4y4=0,即x3x4+y3y4=0$⇒2{x_3}{x_4}-b({x_3}+{x_4})+{b^2}=0$,
∴b=0或-8 经检验,符合题意
∴b=0或-8 …(6分)
(Ⅲ) 由题意知,|m|≥1.
易知切线l的斜率存在,设切线l的方程为y=kx+m,
由$\left\{\begin{array}{l}y=kx+m\\ \frac{{y_{\;}^2}}{4}+x_{\;}^2=1\end{array}\right.$,整理得:$(k_{\;}^2+4)x_{\;}^2+2{k^{\;}}mx+{m^2}-4=0$,…(7分)
设A,B两点的坐标分别为(x1,y1),(x2,y2),则${x_1}+{x_2}=-\frac{2km}{{{k^2}+4}}$,${x_1}{x_2}=\frac{{{m^2}-4}}{{{k^2}+4}}$.…(8分)
又由l与圆x2+y2=1相切,
∴$\frac{|m|}{{\sqrt{{k^2}+1}}}=1$,k2=m2-1.
∴$|AB|=\sqrt{1+{k^2}}\sqrt{{{({x_1}+{x_2})}^2}-4{x_1}{x_2}}$=$\sqrt{(1+{k^2})[\frac{{4{k^2}{m^2}}}{{{{({k^2}+4)}^2}}}-\frac{{4({m^2}-4)}}{{{k^2}+4}}]}=\frac{{4\sqrt{3}|m|}}{{{m^2}+3}}$…(10分)
${S_{△AOB}}=\frac{1}{2}|{AB}|=\frac{{2\sqrt{3}|m|}}{{{m^2}+3}}$,|m|≥1.…(11分)
${S_{△AOB}}=\frac{{2\sqrt{3}}}{{|m|+\frac{3}{|m|}}}≤\frac{{2\sqrt{3}}}{{2\sqrt{|m|\frac{3}{|m|}}}}=1$(当且仅当$m=±\sqrt{3}$时取等号),
∴当$m=±\sqrt{3}$时,S△AOB的最大值为1.…(12分)
点评 本题考查椭圆的标准方程,直线与椭圆的位置关系,考查韦达定理,弦长公式,三角形面积公式与基本不等式的性质综合应用,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (1,1.25) | B. | (1.25,1.5) | C. | (1.5,2) | D. | 不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{3}$ | B. | 向右平移$\frac{π}{3}$ | C. | 向左平移$\frac{π}{6}$ | D. | 向右平移$\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
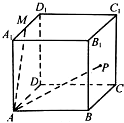 在棱长为1的正方体ABCD-A1B1C1D1中,M是A1D1的中点,点P在侧面 BCC1B1上运动.现有下列命题:
在棱长为1的正方体ABCD-A1B1C1D1中,M是A1D1的中点,点P在侧面 BCC1B1上运动.现有下列命题:| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,将1,2,3,4任意排成2行2列的田字形数表.
如图,将1,2,3,4任意排成2行2列的田字形数表.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com