
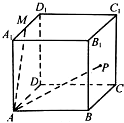
 ���ⳤΪ1��������ABCD-A1B1C1D1�У�M��A1D1���е㣬��P�ڲ��� BCC1B1���˶��������������⣺
���ⳤΪ1��������ABCD-A1B1C1D1�У�M��A1D1���е㣬��P�ڲ��� BCC1B1���˶��������������⣺| A�� | 4 | B�� | 3 | C�� | 2 | D�� | 1 |
���� ��BD1����AB1C���ɵ�P����AB1C����BCC1B1�Ľ������жϢ���ȷ����ƽ�������켣��Բ�жϢ���ȷ������ƽ���Բ����ɵ�P��켣����������˫���ߵ�һ֧��˵���۴�������Բ����˵���ܲ���ȷ�������ռ�����ϵ����|PF|=|PG|��ʽ�������P�Ĺ켣˵���ݴ���
��� �⣺ ���ڢ٣���BD1����AB1C���ද��P�Ĺ켣����������ֱ��B1C������ȷ��
���ڢ٣���BD1����AB1C���ද��P�Ĺ켣����������ֱ��B1C������ȷ��
���ڢڣ����㵽��A�ľ���Ϊ$\frac{2\sqrt{3}}{3}$�ĵ㼯�����PӦΪƽ����������ýغۣ����켣��������ΪԲ������ȷ��
���ڢۣ�����������MAP=��MAC1 �ĵ�PӦΪ��AMΪ�ᣬ��AC1 Ϊĸ�ߵ�Բ��ƽ��BB1C1C��һ������AMƽ�е�ƽ�棬
�ֵ�P��BB1C1C���ڵ�ƽ���ϣ���P��켣����������˫����һ֧��
�۴���
���ڢܣ�P��ֱ��C1D1 �ľ��룬
������C1�ľ����뵽ֱ��BC�ľ����Ϊ1��2��
�ද��P�Ĺ켣������������C1 Ϊ���㣬��ֱ��BCΪ�ߵ���Բ���ܲ���ȷ��
���ڢݣ���ͼ�����ռ�ֱ������ϵ����PE��BC��EF��AD��PG��CC1������PF��
���P������x��y��0������|PF|=|PG|����$\sqrt{1+{y}^{2}}$=|x|����x2-y2=1��
��P��켣����������˫���ߣ��ݴ���
��ѡC��
���� ���⿼�������������ж���Ӧ�ã�������Բ���ߵĶ���ͷ��̣�������ѧ���Ŀռ�����������˼ά���������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 18 | B�� | 12 | C�� | 7 | D�� | 24 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{\sqrt{3}}{2}$ | B�� | -$\frac{\sqrt{3}}{2}$ | C�� | $\frac{1}{2}$ | D�� | -$\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com