
分析 (1)由已知中直线$\sqrt{3}$x+y-$\sqrt{3}$=0经过椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右焦点和上顶点,可得椭圆C的标准方程;
(2)设出直线方程,代入椭圆方程,利用韦达定理,及∠AOB为钝角,建立不等式,即可求得直线l的斜率k的取值范围;
(3)由切线的性质,结合四点共圆判断可得P,M,O,N四点共圆,可得其圆心O'($\frac{{x}_{p}}{2}$,$\frac{{y}_{p}}{2}$),求得圆方程,由两圆方程相减可得相交弦方程,由题意可得P1P2的方程为$\frac{x}{m}+\frac{y}{n}$=1,求得P的坐标,代入椭圆方程即可得证.
解答 解:(1)直线$\sqrt{3}$x+y-$\sqrt{3}$=0经过椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右焦点和上顶点.
故c=1,b=$\sqrt{3}$,
故a=2,
故椭圆C的标准方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(2)显然直线x=0不满足条件,可设直线l:y=kx-2,A(x1,y1),B(x2,y2)
直线代入椭圆方程,消去y可得(3+4k2)x2-16kx+4=0
∵△=(16k)2-12×(3+4k2)>0,∴k<-$\frac{3\sqrt{13}}{26}$或k>$\frac{3\sqrt{13}}{26}$
x1+x2=$\frac{16k}{3+4{k}^{2}}$,x1x2=$\frac{4}{3+4{k}^{2}}$
∴y1y2=(kx1-2)(kx2-2)=k2x1x2-2k(x1+x2)+4=$\frac{12-16{k}^{2}}{3+4{k}^{2}}$
由于∠AOB为钝角,x1x2+y1y2<0,∴$\frac{16-16{k}^{2}}{3+4{k}^{2}}$<0,
∴k<-1或k>1
∴直线L的斜率的取值范围是k<-1或k>1
证明:(3)因为MN为切点,所以OM⊥PM,ON⊥PN,
所以P,M,O,N四点共圆,
其圆心O'($\frac{{x}_{p}}{2}$,$\frac{{y}_{p}}{2}$),方程为(x-$\frac{{x}_{p}}{2}$)2+(y-$\frac{{y}_{p}}{2}$)2=$\frac{{x}_{p}^{2}+{y}_{p}^{2}}{4}$,
整理得x2+y2-xxP-yyP=0,
MN是圆O与圆O'的交点,
联立圆O:x2+y2=2的方程得xxP+yyP=2,
直线MN在x轴,y轴上的截距分别为m,n,
可得直线MN的方程为$\frac{x}{m}+\frac{y}{n}$=1,
得xP=$\frac{2}{m}$,yP=$\frac{2}{n}$,
因为P(xP,yP)在椭圆$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$上,
则$\frac{{(\frac{2}{m})}^{2}}{4}+\frac{{(\frac{2}{n})}^{2}}{3}=1$,
整理得$\frac{1}{4{m}^{2}}+\frac{1}{3{n}^{2}}$=1
点评 本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查韦达定理的运用,考查学生的计算能力,属于中档题.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:选择题
| A. | -2<m<4 | B. | -4<m<2 | C. | 2<m<4 | D. | -4<m<4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
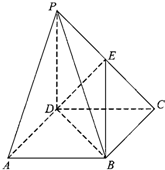 《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.
《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
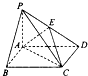 如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点.
如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com