
分析 通过判定函数f(x)=2x-2-x)=2x-$(\frac{1}{2})$x在R上单调递增、奇函数,脱掉”f“,转化为恒成立问题,分离参数求解.
解答 解:∵函数f(x)=2x-2-x)=2x-$(\frac{1}{2})$x在R上单调递增,又∵f(-x)=-(2x-2-x)=-f(x),故f(x)是奇函数,若对任意的x∈[1,3],不等式f(x2+tx)+f(4-x)>0恒成立,⇒对任意的x∈[1,3],不等式f(x2+tx)>f(-4+x)恒成立,
⇒对任意的x∈[1,3],x2+(t-1)x+4>0⇒(t-1)x>-x2-4⇒t-1>-(x+$\frac{4}{x})$,
∵$g(x)=x+\frac{4}{x}≥2\sqrt{x•\frac{4}{x}}=4…(x=2时取等号)$,∴t-1>-4,即t>-3.
故答案为:(-3.+∞)
点评 本题考查了函数的单调性、奇函数,恒成立问题,分离参数法,属于中档题.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:解答题
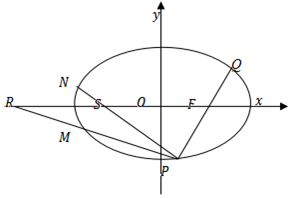 如图,椭圆C:$\frac{x^2}{9}$+$\frac{y^2}{b^2}$=1(0<b<3)的右焦点为F,P为椭圆上一动点,连接PF交椭圆于Q点,且|PQ|的最小值为$\frac{8}{3}$.
如图,椭圆C:$\frac{x^2}{9}$+$\frac{y^2}{b^2}$=1(0<b<3)的右焦点为F,P为椭圆上一动点,连接PF交椭圆于Q点,且|PQ|的最小值为$\frac{8}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 光明超市某种商品11月份(30天,11月1日为第一天)的销售价格P(单位:元)与时间t(单位:天,其中)组成有序实数对(t,P),点(t,P)落在如图所示的线段上.该商品日销售量Q(单位:件)与时间t(单位:天,其中t∈N)满足一次函数关系,Q与t的部分数据如表所示.
光明超市某种商品11月份(30天,11月1日为第一天)的销售价格P(单位:元)与时间t(单位:天,其中)组成有序实数对(t,P),点(t,P)落在如图所示的线段上.该商品日销售量Q(单位:件)与时间t(单位:天,其中t∈N)满足一次函数关系,Q与t的部分数据如表所示.| 第t天 | 10 | 17 | 21 | 30 |
| Q(件) | 180 | 152 | 136 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com