
分析 (1)把原等式展开两角和与差的余弦,然后化弦为切得答案;
(2)利用余弦定理及正弦定理,把$\frac{S}{{a}^{2}+{b}^{2}-{c}^{2}}$化为含有tanC的代数式,然后利用基本不等式求解.
解答 (1)证明:由$\frac{17}{15}$cos(A+B)-cos(A-B)=0,得
17cosAcosB-17sinAsinB-15cosAcosB-15sinAsinB=0,
即2cosAcosB=32sinAsinB,
∴tanA•tanB=$\frac{1}{16}$;
(2)解:∵c2=a2+b2-2ab•cosC,且S=$\frac{1}{2}ab•sinC$,
∴$\frac{S}{{a}^{2}+{b}^{2}-{c}^{2}}$=$\frac{\frac{1}{2}ab•sinC}{2ab•cosC}$=$\frac{1}{4}tanC$,
而tanC=-tan(A+B)=$-\frac{tanA+tanB}{1-tanAtanB}$=$-\frac{tanA+tanB}{1-\frac{1}{16}}=-\frac{16}{15}(tanA+tanB)$$≤-\frac{16}{15}×2\sqrt{tanAtanB}=-\frac{8}{15}$,
则$\frac{S}{{a}^{2}+{b}^{2}-{c}^{2}}=\frac{1}{4}tanC≤-\frac{2}{15}$(当且仅当tanA=tanB=$\frac{1}{4}$时取等号).
点评 本题考查两角和与差的余弦及正切,考查数学转化思想方法,训练了利用基本不等式求最值,是中档题.


科目:高中数学 来源: 题型:解答题
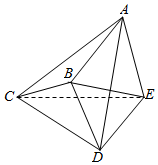 在如图所示的几何体ABCDE中,AE⊥平面DCE,BE=$\sqrt{6}$,DC=4,BD=2,CE=2$\sqrt{3}$,∠BCD=30°,CE⊥AD.
在如图所示的几何体ABCDE中,AE⊥平面DCE,BE=$\sqrt{6}$,DC=4,BD=2,CE=2$\sqrt{3}$,∠BCD=30°,CE⊥AD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{a}$=(-3,5),$\overrightarrow{b}$=(-1,5) | B. | $\overrightarrow{a}$=(3,2),$\overrightarrow{b}$=(-3,-2) | C. | $\overrightarrow{a}$=(3,4),$\overrightarrow{b}$=(4,-3) | D. | $\overrightarrow{a}$=(-3,3),$\overrightarrow{b}$=(-1,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,两同心圆(圆心在原点)分别与OA、OB交于A、B两点,其中A($\sqrt{2}$,1),|OB|=$\sqrt{6}$,阴影部分为两同心圆构成的扇环,已知扇环的面积为$\frac{3π}{4}$.
如图,两同心圆(圆心在原点)分别与OA、OB交于A、B两点,其中A($\sqrt{2}$,1),|OB|=$\sqrt{6}$,阴影部分为两同心圆构成的扇环,已知扇环的面积为$\frac{3π}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 96个 | B. | 78个 | C. | 72个 | D. | 36个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 7 | C. | -4 | D. | -7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{3}{4}$ | B. | $\frac{3}{4}$ | C. | $-\frac{4}{3}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com