
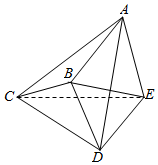
 在如图所示的几何体ABCDE中,AE⊥平面DCE,BE=$\sqrt{6}$,DC=4,BD=2,CE=2$\sqrt{3}$,∠BCD=30°,CE⊥AD.
在如图所示的几何体ABCDE中,AE⊥平面DCE,BE=$\sqrt{6}$,DC=4,BD=2,CE=2$\sqrt{3}$,∠BCD=30°,CE⊥AD.分析 (Ⅰ)过B作BF⊥CD于F,利用线面垂直的判定定理证明,BF∥AE,即可证明AE∥平面BCD;
(Ⅱ)若AE=4$\sqrt{3}$,根据二面角平面角的定义作出二面角的平面角即可求二面角D-AC-E(锐角)的余弦值.
解答 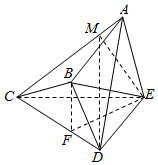 (Ⅰ)证明:∵DC=4,BD=2,∠BCD=30°,
(Ⅰ)证明:∵DC=4,BD=2,∠BCD=30°,
∴△BCD为直角三角形,则CB⊥BD,则BC=2$\sqrt{3}$,
∵CE=2$\sqrt{3}$,CE⊥AD,AE⊥平面DCE,
∴AE⊥CE,
则CE⊥平面ADE,
则CE⊥DE,
则DE=$\sqrt{C{D}^{2}-C{E}^{2}}$=2,
∵BC=CE,DE=DE,∠ABD=∠CED=90°,
∴△CED≌△CBD,
过B作BF⊥CD于F,连接EF,则EF⊥CD,
则BF=EF=BC•sin30°=$\sqrt{3}$,
∵BE=$\sqrt{6}$
∴BF2+EF2=BE2,即BF⊥EF,
∵BF⊥CD,∴BF⊥平面CDE,
∵AE⊥平面DCE,∴BF∥AE,
∵AE?平面BCD,∴AE∥平面BCD;
(Ⅱ)若AE=4$\sqrt{3}$,
由(Ⅰ)知,DE⊥平面ACE,过E作EM⊥AC于M,连接DM,
则∠EMD是二面角D-AC-E(锐角)的平面角,
∵CE=2$\sqrt{3}$,AE=4$\sqrt{3}$,
∴AC=2$\sqrt{15}$,则EM=$\frac{AE•CE}{AC}$=$\frac{4\sqrt{3}•2\sqrt{3}}{2\sqrt{15}}$=$\frac{12}{\sqrt{15}}$,
则DM=$\sqrt{M{E}^{2}+D{E}^{2}}$=$\sqrt{(\frac{12}{\sqrt{15}})^{2}+{2}^{2}}$=$\frac{4\sqrt{85}}{5}$,则cos∠EMD=$\frac{ME}{DM}$=$\frac{\sqrt{51}}{17}$,
二面角D-AC-E(锐角)的余弦值是$\frac{\sqrt{51}}{17}$.
点评 本题主要考查线面平行的判定,以及二面角的求解,利用二面角的定义作出平面角是解决本题的关键.本题也可以建立坐标系,利用向量法进行求解,综合性较强,运算量较大.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
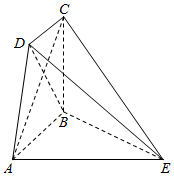 如图,五面体ABCDE中,AB∥CD,CB⊥平面ABE,AE⊥AB,AB=AE=2,BC=$\sqrt{2}$,CD=1.
如图,五面体ABCDE中,AB∥CD,CB⊥平面ABE,AE⊥AB,AB=AE=2,BC=$\sqrt{2}$,CD=1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | Cn=4n-3 | B. | Cn=8n-1 | C. | Cn=4n-5 | D. | Cn=8n-9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
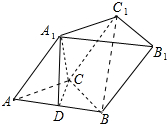 如图,三棱柱ABC-A1B1C1中,A1C⊥底面ABC,∠ACB=120°,A1C=AC=BC=2,D为AB中点.
如图,三棱柱ABC-A1B1C1中,A1C⊥底面ABC,∠ACB=120°,A1C=AC=BC=2,D为AB中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com