
分析 ①根据函数的对应法则,可得不管x是有理数还是无理数,均有f(f(x))=1;②根据函数奇偶性的定义,可得f(x)是偶函数;③根据函数的表达式,结合有理数和无理数的性质;④取x1=-$\frac{\sqrt{3}}{3}$,x2=0,x3=$\frac{\sqrt{3}}{3}$,可得A($\frac{\sqrt{3}}{3}$,0),B(0,1),C(-$\frac{\sqrt{3}}{3}$,0),三点恰好构成等边三角形.
解答 解:①∵当x为有理数时,f(x)=1;当x为无理数时,f(x)=0
∴当x为有理数时,ff((x))=f(1)=1;当x为无理数时,f(f(x))=f(0)=1
即不管x是有理数还是无理数,均有f(f(x))=1,故①不正确;
接下来判断三个命题的真假
②∵有理数的相反数还是有理数,无理数的相反数还是无理数,
∴对任意x∈R,都有f(-x)=f(x),故②正确;
③若x是有理数,则x+T也是有理数; 若x是无理数,则x+T也是无理数
∴根据函数的表达式,任取一个不为零的有理数T,f(x+T)=f(x)对x∈R恒成立,故③正确;
④取x1=-$\frac{\sqrt{3}}{3}$,x2=0,x3=$\frac{\sqrt{3}}{3}$,可得f(x1)=0,f(x2)=1,f(x3)=0
∴A($\frac{\sqrt{3}}{3}$,0),B(0,1),C(-$\frac{\sqrt{3}}{3}$,0),恰好△ABC为等边三角形,故④正确.
故答案为:②③④.
点评 本题给出特殊函数表达式,求函数的值并讨论它的奇偶性,着重考查了有理数、无理数的性质和函数的奇偶性等知识,属于中档题.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:高中数学 来源: 题型:解答题
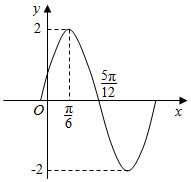 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
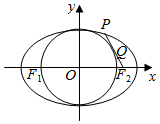 如图,F1,F2是椭圆C;$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,点P在椭圆C上,线段PF2与圆x2+y2=b2相切于点Q,且点Q为线段PF2的中点,则$\frac{{a}^{2}+{e}^{2}}{3b}$(e为椭圆的离心率)的最小值为( )
如图,F1,F2是椭圆C;$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,点P在椭圆C上,线段PF2与圆x2+y2=b2相切于点Q,且点Q为线段PF2的中点,则$\frac{{a}^{2}+{e}^{2}}{3b}$(e为椭圆的离心率)的最小值为( )| A. | $\frac{\sqrt{5}}{3}$ | B. | $\frac{\sqrt{5}}{4}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{\sqrt{6}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com