
已知函数
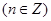 满足
满足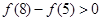 .
.
(1)求 的解析式;
的解析式;
(2)对于(1)中得到的函数 ,试判断是否存在
,试判断是否存在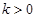 ,使
,使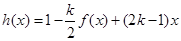 在区间
在区间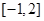 上的值域为
上的值域为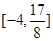 ?若存在,求出
?若存在,求出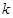 ;若不存在,请说明理由.
;若不存在,请说明理由.
科目:高中数学 来源: 题型:解答题
对于定义域为A的函数f(x),如果任意的x1,x2∈A,当x1<x2时,都有f(x1)<f(x2),则称函数f(x)是A上的严格增函数;函数f(k)是定义在N*上,函数值也在N*中的严格增函数,并且满足条件f(f(k))=3k.
(1)证明:f(3k)=3f(k);
(2)求f(3k-1)(k∈N*)的值;
(3)是否存在p个连续的自然数,使得它们的函数值依次也是连续的自然数;若存在,找出所有的p值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知 是正数,
是正数, ,
, ,
, .
.
(Ⅰ)若 成等差数列,比较
成等差数列,比较 与
与 的大小;
的大小;
(Ⅱ)若 ,则
,则 三个数中,哪个数最大,请说明理由;
三个数中,哪个数最大,请说明理由;
(Ⅲ)若 ,
, ,
, (
( ),且
),且 ,
, ,
, 的整数部分分别是
的整数部分分别是

 求所有
求所有 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
己知函数f(x)=ex,x R.
R.
(1)若直线y=kx+1与f(x)的反函数图象相切,求实数k的值;
(2)设x﹥0,讨论曲线y=f(x)与曲线y=mx2(m﹥0)公共点的个数;
(3)设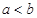 ,比较
,比较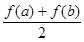 与
与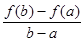 的大小并说明理由。
的大小并说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某产品生产厂家根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产产品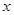 (百台),其总成本为
(百台),其总成本为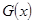 (万元),其中固定成本为2.8万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本)。销售收入
(万元),其中固定成本为2.8万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本)。销售收入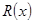 (万元)满足
(万元)满足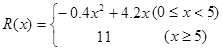 ,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
分别写出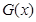 和利润函数
和利润函数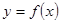 的解析式(利润=销售收入—总成本);
的解析式(利润=销售收入—总成本);
工厂生产多少台产品时,可使盈利最多?并求出此时每台产品的售价。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com