
分析 (1)设等差数列{an}的公差为d,由等差数列的通项公式可得首项和公差的方程,解方程即可得到所求;
(2)求得bn=2${\;}^{{a}_{n}-2}$+n=2n+n,运用数列的求和方法:分组求和,结合等比数列和等差数列的求和公式,计算即可得到所求和.
解答 解:(1)设等差数列{an}的公差为d,
由a2=4,a4+a7=15.
得a1+d=4,(a1+3d)+(a1+6d)=15,
解得a1=3,d=1,
所以an=a1+(n-1)d=3+n-1=n+2;
(2)由(1)可得bn=2${\;}^{{a}_{n}-2}$+n=2n+n,
所以b1+b2+b3+…+b10=(2+1)+(22+2)+(23+3)+…+(210+10)
=(2+22+23+…+210)+(1+2+3+…+10)
=$\frac{2(1-{2}^{10})}{1-2}$+$\frac{(1+10)×10}{2}$=(211-2)+55=211+53=2101.
点评 本题考查等差数列的通项公式和求和公式,以及等比数列的求和公式的运用,考查数列的求和方法:分组求和,以及运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
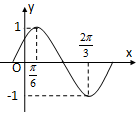 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x-y=0 | B. | 2x-y-2=0 | C. | x+2y-3=0 | D. | x+2y-5=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
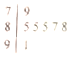 在华中师大一附中首届数学节的演讲比赛中,七位评委为某参赛教师打出的分数的茎叶图如图所示,去掉最高分和最低分后,这位老师得分的方差为( )
在华中师大一附中首届数学节的演讲比赛中,七位评委为某参赛教师打出的分数的茎叶图如图所示,去掉最高分和最低分后,这位老师得分的方差为( )| A. | 1.14 | B. | 1.6 | C. | 2.56 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 考拉兹猜想又名3n+1猜想,是指对于每一个正整数,如果它是奇数,则对它乘3再加1;如果它是偶数,则对它除以2.如此循环,最终都能得到1.阅读如图所示的程序框图,运行相应程序,输出的结果i=( )
考拉兹猜想又名3n+1猜想,是指对于每一个正整数,如果它是奇数,则对它乘3再加1;如果它是偶数,则对它除以2.如此循环,最终都能得到1.阅读如图所示的程序框图,运行相应程序,输出的结果i=( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com