
分析 先利用条件得出A、B两点连线的斜率k,再利用A、B两点的中点在直线y=x+m求出关于m以及x2,x1的方程,再与已知条件联立求出实数m的值.
解答 解:由题意,$\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}$=-1,y2-y1=2(x22-x12),
∴x1+x2=-$\frac{1}{2}$,
$(\frac{{{x_2}+{x_1}}}{2},\frac{{{y_2}+{y_1}}}{2})$在直线y=x+m上,即$\frac{{{y_2}+{y_1}}}{2}=\frac{{{x_2}+{x_1}}}{2}+m,{y_2}+{y_1}={x_2}+{x_1}+2m$,
所以有2(x22+x12)=x2+x1+2m,即2[(x2+x1)2-2x2x1]=x2+x1+2m,
∴2m=4,∴m=2,
故答案为2.
点评 本题是对直线与抛物线位置关系以及点与直线位置的综合考查.当两点关于已知直线对称时,有两条结论,一是两点的中点在已知直线上;二是两点的连线与已知直线垂直.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{3}+1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
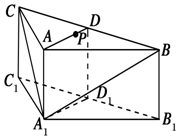 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB=AC,D,D1分别是线段BC,B1C1的中点,P是线段AD上异于端点的点.
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB=AC,D,D1分别是线段BC,B1C1的中点,P是线段AD上异于端点的点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com