
(本小题满分14分)(文科)已知曲线
 的离心率
的离心率 ,直线
,直线 过
过 、
、 两点,原点
两点,原点 到
到 的距离是
的距离是 .
.
(Ⅰ)求双曲线的方程;
(Ⅱ)过点 作直线
作直线 交双曲线于
交双曲线于 两点,若
两点,若 ,求直线
,求直线 的方程.
的方程.
(Ⅰ)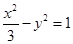 (Ⅱ)
(Ⅱ) 或
或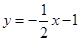
解析试题分析:(Ⅰ)依题意,直线 的方程为:
的方程为: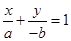 ,即
,即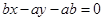 .
.
由原点 到
到 的距离是
的距离是 ,得
,得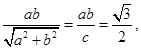
又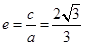 ,
,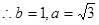 .
.
故所求双曲线方程为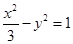 . ……6分
. ……6分
(Ⅱ)显然直线 不与
不与 轴垂直,设
轴垂直,设 方程为
方程为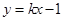 ,
,
则点 坐标(
坐标(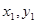 )、(
)、(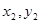 )是方程组
)是方程组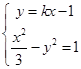 的解,
的解,
消去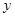 ,得
,得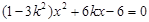 ①
①
依题意知,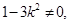 由根与系数关系,知
由根与系数关系,知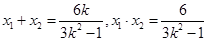 ……10分
……10分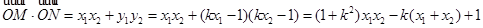
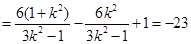 ,解得
,解得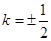 ,
,
当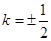 时,方程①有两个不等的实数根
时,方程①有两个不等的实数根
故直线 方程为
方程为 或
或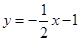 . ……14分
. ……14分
考点:本小题主要考查了双曲线的标准方程与几何性质、直线与双曲线的位置关系、平面向量知识以及数形结合思想和划归思想,考查学生综合运用所学知识解决问题的能力和运算求解能力.
点评:解答这种习题时,通常用到设而不求的思想方法,另外,圆锥曲线的题目运算量一般都比较大,要注意数形结合简化运算,也要在实际的学习中多多练习.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案科目:高中数学 来源: 题型:解答题
(本题16分)在平面直角坐标系 中,
中,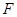 是抛物线
是抛物线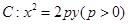 的焦点,
的焦点,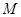 是抛物线
是抛物线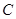 上位于第一象限内的任意一点,过
上位于第一象限内的任意一点,过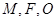 三点的圆的圆心为
三点的圆的圆心为 ,点
,点 到抛物线
到抛物线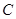 的准线的距离为
的准线的距离为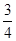 .
.
(Ⅰ)求抛物线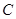 的方程;
的方程;
(Ⅱ)是否存在点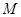 ,使得直线
,使得直线 与抛物线
与抛物线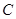 相切于点
相切于点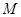 ?若存在,求出点
?若存在,求出点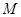 的坐标;若不存在,说明理由;
的坐标;若不存在,说明理由;
(Ⅲ)若点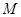 的横坐标为
的横坐标为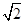 ,直线
,直线 与抛物线
与抛物线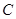 有两个不同的交点
有两个不同的交点 ,
,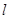 与圆
与圆 有两个不同的交点
有两个不同的交点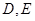 ,求当
,求当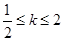 时,
时,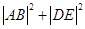 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(12分)已知椭圆 的离心率
的离心率 ,过右焦点
,过右焦点 的直线
的直线 与椭圆
与椭圆 相交于
相交于 两点,当直线
两点,当直线 的斜率为1时,坐标原点
的斜率为1时,坐标原点 到直线
到直线 的距离为
的距离为 .
.
(1)求椭圆 的方程
的方程
(2)椭圆 上是否存在点
上是否存在点 ,使得当直线
,使得当直线 绕点
绕点 转到某一位置时,有
转到某一位置时,有 成立?若存在,求出所有满足条件的点
成立?若存在,求出所有满足条件的点 的坐标及对应直线方程;若不存在,请说明理由。
的坐标及对应直线方程;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分13分)在平面直角坐标系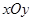 中,已知椭圆
中,已知椭圆 :
: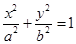 (
( )的左焦点为
)的左焦点为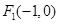 ,且点
,且点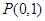 在
在 上.
上.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)已知直线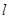 的斜率为2且经过椭圆
的斜率为2且经过椭圆 的左焦点.求直线
的左焦点.求直线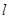 与该椭圆
与该椭圆 相交的弦长。
相交的弦长。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)
如图,已知椭圆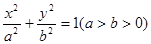 的长轴为
的长轴为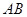 ,过点
,过点 的直线
的直线 与
与 轴垂直,直线
轴垂直,直线 所经过的定点恰好是椭圆的一个顶点,且椭圆的离心率
所经过的定点恰好是椭圆的一个顶点,且椭圆的离心率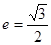

(1)求椭圆的标准方程;
(2)设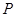 是椭圆上异于
是椭圆上异于 、
、 的任意一点,
的任意一点, 轴,
轴,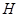 为垂足,延长
为垂足,延长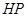 到点
到点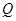 使得
使得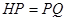 ,连接
,连接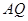 并延长交直线
并延长交直线 于点
于点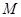 ,
,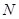 为
为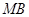 的中点.试判断直线
的中点.试判断直线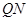 与以
与以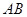 为直径的圆
为直径的圆 的位置关系.
的位置关系.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
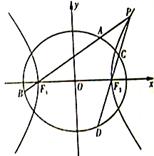
(本小题满分12分)如图,已知椭圆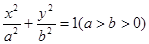 的离心率为
的离心率为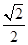 ,以该椭圆上的点和椭圆的左、右焦点
,以该椭圆上的点和椭圆的左、右焦点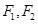 为顶点的三角形的周长为
为顶点的三角形的周长为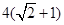 .一等轴双曲线的顶点是该椭圆的焦点,设
.一等轴双曲线的顶点是该椭圆的焦点,设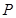 为该双曲线上异于顶点的任一点,直线
为该双曲线上异于顶点的任一点,直线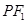 和
和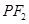 与椭圆的交点分别为
与椭圆的交点分别为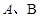 和
和 .
.
(Ⅰ)求椭圆和双曲线的标准方程;
(Ⅱ)设直线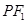 、
、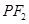 的斜率分别为
的斜率分别为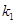 、
、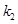 ,证明
,证明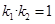 ;
;
(Ⅲ)是否存在常数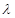 ,使得
,使得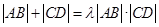 恒成立?若存在,求
恒成立?若存在,求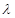 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com