
| A. | a=1,b=1 | B. | a=-1,b=-1 | C. | a=1,b=-1 | D. | a=-1,b=1 |
分析 由基本不等式求得g(x)的最小值及取最小值时x0的值,再利用导数求得使f(x)取得最值时的a值,然后再代入f(x0)=2求得b值.
解答 解:∵当x∈[$\frac{1}{2}$,2]时,g(x)=x+$\frac{1}{x}$≥2,当且仅当x=1时取等号,
∴x0=1,g(x0)=2;
∵f′(x)=2ax+2(a-1)$-\frac{2}{x}$=$\frac{2(ax-1)(x+1)}{x}$,x∈[$\frac{1}{2}$,2],
①当a≤0时,f′(x)<0,故函数f(x)在[$\frac{1}{2}$,2]上单调递减,不合题意;
②当a>0时,由f′(x)<0,得0$<x<\frac{1}{a}$,f′(x)<0,得x$>\frac{1}{a}$,
故函数f(x)在(0,$\frac{1}{a}$)上单调递减,在($\frac{1}{a}$,+∞)上单调递增,依题意得$\frac{1}{a}=1$,即a=1.
$f({x}_{0})=f(1)=a•{1}^{2}+2(a-1)•1-2ln1+b=3a-2+b=2$,解得:b=1.
故选:A.
点评 本题是新定义题,考查了利用基本不等式求函数的最值,训练了利用导数求函数的最值,题目综合性强,关键是对题意的理解,属中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$:1 | B. | 1:$\sqrt{2}$ | C. | $\sqrt{2}$:$\sqrt{3}$ | D. | $\sqrt{3}$:$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
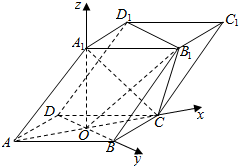 如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=AA1=$\sqrt{2}$.平面OCB1的法向量$\overrightarrow{n}$=(x,y,z)为( )
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=AA1=$\sqrt{2}$.平面OCB1的法向量$\overrightarrow{n}$=(x,y,z)为( )| A. | (0,1,1) | B. | (1,-1,1) | C. | (0,1,-1) | D. | (-1,-1,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$\frac{1}{x}$ | B. | y=-x+$\frac{1}{x}$ | ||
| C. | y=-x|x| | D. | y=$\left\{\begin{array}{l}{-x+1,x>0}\\{-x-1,x≤0}\end{array}\right.$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com