
 ?请说明理由!
?请说明理由! =
=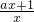 ,
,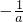 ,当0<x<-
,当0<x<- 时,f′(x)>0,f(x)在(0,-
时,f′(x)>0,f(x)在(0,- )上单调递增;当x>-
)上单调递增;当x>- 时,f′(x)<0,f(x)在(-
时,f′(x)<0,f(x)在(- ,+∞)上单调递减.
,+∞)上单调递减. <1即a<-1,则x>1时,f(x)<f(1)=0,故a<-1不合题意;若-
<1即a<-1,则x>1时,f(x)<f(1)=0,故a<-1不合题意;若- >1,即-1<a<0,则x<1时,f(x)<f(1)=0,故-1<a<0不合题意.
>1,即-1<a<0,则x<1时,f(x)<f(1)=0,故-1<a<0不合题意. =
=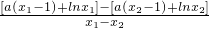 =
=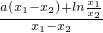 =a+
=a+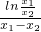 .
. ,令g(x)=f′(x)-
,令g(x)=f′(x)- =(a+
=(a+ )-(a+
)-(a+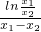 )=
)= -
-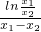 .
. -
-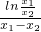 =
=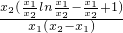 ,g(x2)=
,g(x2)= -
-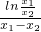 =
=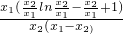 .
.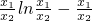 +1>0,
+1>0,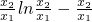 +1>0.又
+1>0.又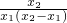 >0,
>0,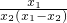 <0,
<0, .
. ,则问题转化为判断函数g(x)在(x1,x2)上是否存在零点x0 ,从而可利用函数存在零点的条件进行判断.
,则问题转化为判断函数g(x)在(x1,x2)上是否存在零点x0 ,从而可利用函数存在零点的条件进行判断.

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:
| a-x2 |
| x |
| 1 |
| 2 |
| 1 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com