
分析 (1)由题意,可得设f(x)=ax2+bx+c,由f(0)=2,f(x+1)-f(x)=x-1,利用待定系数法求解即可.
(2)根据二次函数的性质求解即可.
解答 解:(1)由题意,设f(x)=ax2+bx+c,
∵f(0)=2,
∴c=2,
则f(x)=ax2+bx+2,
由f(x+1)-f(x)=x-1,即a(x+1)2+b(x+1)+2-ax2-bx-2=x-1
可得:a=$\frac{1}{2}$,b=$-\frac{3}{2}$,
∴f(x)的解析式为:f(x)=$\frac{1}{2}$x2$-\frac{3}{2}$x+2
(2)f(x)=$\frac{{{x^2}+2x+a}}{x}$,
∵f(x)>0恒成立,即$\frac{{{x^2}+2x+a}}{x}$>0在x∈[1,+∞),
∵x∈[1,+∞),
转化为x2+2x+a>0,
令g(x)=x2+2x+a=(x+1)2+a-1,
其对称轴x=-1,开口向上,
可知x在(-1,+∞)是单调递增.
∴只需g(1)>0即可.
得3+a>0,
∴a>-3
故得实数a的取值范围(-3,+∞).
点评 本题考查了函数解析式的求法,利用了待定系数法,同时考查了二次函数的恒成立问题.属于基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
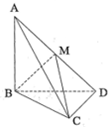 如图,三棱锥A-BCD中,AB⊥平面BCD,CD⊥BD.
如图,三棱锥A-BCD中,AB⊥平面BCD,CD⊥BD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
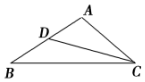 如图所示,给出下列条件:
如图所示,给出下列条件:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
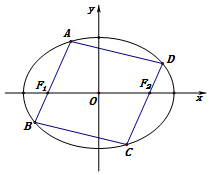 已知椭圆E的方程是$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,左、右焦点分别是F1、F2,在椭圆E上有一动点A,过A、F1作一个平行四边形,使顶点A、B、C、D都在椭圆E上,如图所示.
已知椭圆E的方程是$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,左、右焦点分别是F1、F2,在椭圆E上有一动点A,过A、F1作一个平行四边形,使顶点A、B、C、D都在椭圆E上,如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 时间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期七 |
| 车流量x(万辆) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| PM2.5的浓度y(微克/立方米) | 28 | 30 | 35 | 41 | 49 | 56 | 62 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com