
分析 根据总人数和分的段数得到分段后每一段的人数是40人,得到最后一段的第一个编号是760,写出最后一组的号,根据最后一个入样的编号为789,即可依次写出结果.
解答 解:利用系统抽样从800个个体中抽取20个个体,
因此分段后每一段的人数是40人,
∴最后一段的第一个编号是799-40+1=760,
∴最后一段的编号是760~799,
∵最后一个入样的编号为789,789-760+1=30,
故入样的应是每组第30个数
则前三组人样编号分别是029,049,069.
故答案为:029,049,069.
点评 本题考查系统抽样,要从容量为N的总体中抽取容量为n的样本,可将总体分成均衡的若干部分,然后按照预先制定的规则,从每一部分抽取一个个体,得到所需要的样本.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:高中数学 来源: 题型:解答题
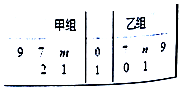 某车间将10名技工平均分成甲、乙两组加工某种零件,在单位时间内每个技工加工的合格零件数的统计数据的茎叶图如图所示.已知两组技工在单位时间内加工的合格零件平均数都为9.
某车间将10名技工平均分成甲、乙两组加工某种零件,在单位时间内每个技工加工的合格零件数的统计数据的茎叶图如图所示.已知两组技工在单位时间内加工的合格零件平均数都为9.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-$\frac{1}{2}$) | B. | (-∞,-1) | C. | (-1,-$\frac{1}{2}$) | D. | (-∞,-2)∪(0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
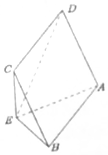 如图,在几何体ABCDE中,ABCD为正方形,CE⊥平面ABE,且异面直线AD、CE所成的角为30°.
如图,在几何体ABCDE中,ABCD为正方形,CE⊥平面ABE,且异面直线AD、CE所成的角为30°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com