
【题目】已知双曲线 ![]() 的两个焦点为
的两个焦点为 ![]() 的曲线C上.
的曲线C上.
(Ⅰ)求双曲线C的方程;
(Ⅱ)记O为坐标原点,过点Q(0,2)的直线l与双曲线C相交于不同的两点E、F,若△OEF的面积为 ![]() ,求直线l的方程.
,求直线l的方程.
【答案】解:(Ⅰ):依题意,由a2+b2=4,得双曲线方程为 ![]() (0<a2<4),
(0<a2<4),
将点(3, ![]() )代入上式,得
)代入上式,得 ![]() .解得a2=18(舍去)或a2=2,
.解得a2=18(舍去)或a2=2,
故所求双曲线方程为 ![]() .
.
(Ⅱ):依题意,可设直线l的方程为y=kx+2,代入双曲线C的方程并整理,
得(1﹣k2)x2﹣4kx﹣6=0.
∵直线I与双曲线C相交于不同的两点E、F,
∴ 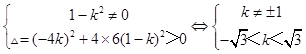
∴k∈(﹣ ![]() )∪(1,
)∪(1, ![]() ).
).
设E(x1,y1),F(x2,y2),则由①式得x1+x2= ![]() ,x1x2=﹣
,x1x2=﹣ ![]() ,
,
于是,|EF|= ![]()
= 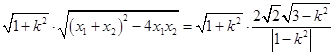
而原点O到直线l的距离d= ![]() ,
,
∴S△OEF=  .
.
若S△OEF= ![]() ,即
,即 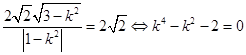 ,解得k=±
,解得k=± ![]() ,
,
满足②.故满足条件的直线l有两条,其方程分别为y= ![]() 和
和 ![]()
【解析】(1)根据题意可得a2+b2=4,得到a和b的关系,把点(3, ![]() )代入双曲线方程,求得a,进而根据a2+b2=4求得b,双曲线方程可得.(2)可设直线l的方程为y=kx+2,代入双曲线C的方程并整理,根据直线I与双曲线C相交于不同的两点E、F,进而可得k的范围,设E(x1,y1),F(x2,y2),根据韦达定理可求得x1+x2和x1x2,进而表示出|EF|和原点O到直线l的距离根据三角形OEF的面积求得k,进而可得直线方程.
)代入双曲线方程,求得a,进而根据a2+b2=4求得b,双曲线方程可得.(2)可设直线l的方程为y=kx+2,代入双曲线C的方程并整理,根据直线I与双曲线C相交于不同的两点E、F,进而可得k的范围,设E(x1,y1),F(x2,y2),根据韦达定理可求得x1+x2和x1x2,进而表示出|EF|和原点O到直线l的距离根据三角形OEF的面积求得k,进而可得直线方程.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】习大大构建的“一带一路”经济带的发展规划已经得到了越来越多相关国家的重视和参与.某市顺潮流、乘东风,闻迅而动,决定利用旅游资源优势,撸起袖子大干一场.为了了解游客的情况,以便制定相应的策略.在某月中随机抽取甲、乙两个景点各10天的游客数,画出茎叶图如下: 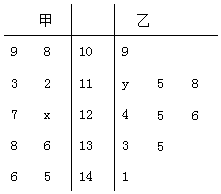
(1)若景点甲中的数据的中位数是125,景点乙中的数据的平均数是124,求x,y的值;
(2)若将图中景点甲中的数据作为该景点较长一段时期内的样本数据.今从这段时期中任取4天,记其中游客数超过120人的天数为ξ,求概率P(ξ≤2);
(3)现从上图的共20天的数据中任取2天的数据(甲、乙两景点中各取1天),记其中游客数不低于115且不高于125人的天数为η,求η的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥E﹣ABCD中,底面ABCD为正方形,AE⊥平面CDE,已知AE=DE=2,F为线段DF的中点. (I)求证:BE∥平面ACF;
(II)求平面BCF与平面BEF所成锐二面角的余弦角.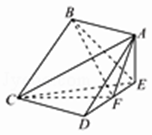
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了得到函数y= ![]() sin(2x﹣
sin(2x﹣ ![]() )的图象,只需将函数y=sinxcosx的图象( )
)的图象,只需将函数y=sinxcosx的图象( )
A.向左平移 ![]() 个单位
个单位
B.向右平移 ![]() 个单位
个单位
C.向左平移 ![]() 个单位
个单位
D.向右平移 ![]() 个单位
个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=8x的焦点为F,准线l与x轴的交点为M,过点M的直线l′与抛物线C的交点为P,Q,延长PF交抛物线C于点A,延长QF交抛物线C于点B,若 ![]() +
+ ![]() =22,则直线l′的方程为 .
=22,则直线l′的方程为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知直线l过定点P(1,1),且倾斜角为 ![]() ,以坐标原点为极点,x轴的正半轴为极轴的坐标系中,曲线C的极坐标方程为
,以坐标原点为极点,x轴的正半轴为极轴的坐标系中,曲线C的极坐标方程为 ![]() .
.
(1)求曲线C的直角坐标方程与直线l的参数方程;
(2)若直线l与曲线C相交于不同的两点A,B,求|AB|及|PA||PB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面上,点A、C为射线PM上的两点,点B、D为射线PN上的两点,则有 ![]() (其中S△PAB、S△PCD分别为△PAB、△PCD的面积);空间中,点A、C为射线PM上的两点,点B、D为射线PN上的两点,点E、F为射线PL上的两点,则有
(其中S△PAB、S△PCD分别为△PAB、△PCD的面积);空间中,点A、C为射线PM上的两点,点B、D为射线PN上的两点,点E、F为射线PL上的两点,则有 ![]() =(其中VP﹣ABE、VP﹣CDF分别为四面体P﹣ABE、P﹣CDF的体积).
=(其中VP﹣ABE、VP﹣CDF分别为四面体P﹣ABE、P﹣CDF的体积). 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx+ ![]() )(x∈R,ω>0)的最小正周期为π,将y=f(x)的图象向左平移|φ|个单位长度,所得函数y=f(x)为偶函数时,则φ的一个值是( )
)(x∈R,ω>0)的最小正周期为π,将y=f(x)的图象向左平移|φ|个单位长度,所得函数y=f(x)为偶函数时,则φ的一个值是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com