
分析 (1)设F1(-c,0),F2(c,0),B(0,b),由题意可得a=2c,再由椭圆的定义和三点共线取得最小值,可得$\sqrt{{c}^{2}+8}$-2a=-1,解方程可得a=2,c=1,求得b,进而得到椭圆方程;
(2)运用直线和圆相切的条件:d=r,求得|CD|=3,联立直线l的方程和椭圆方程,运用韦达定理和判别式大于0,由四边形CMDN的面积S=$\frac{1}{2}$|CD|•|x1-x2|,化简整理,运用基本不等式可得最大值及等号成立的条件,求得直线l的方程.
解答 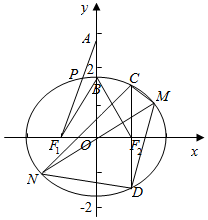 解:(1)设F1(-c,0),F2(c,0),B(0,b),
解:(1)设F1(-c,0),F2(c,0),B(0,b),
由△BF1F2为正三角形,可得|BF1|=|F1F2|,
即有a=2c,①
由椭圆的定义可得2a=|PF1|+|PF2|,
即|PF2|=2a-|PF1|,
则|PA|-|PF2|=|PA|-(2a-|PF1|)=|PA|+|PF1|-2a,
≥|AF1|-2a=$\sqrt{{c}^{2}+8}$-2a,
当A,P,F1共线时,|PA|+|PF1|取得最小值,
即有$\sqrt{{c}^{2}+8}$-2a=-1,②
由①②可得c=1,a=2,b=$\sqrt{3}$,
可得椭圆的方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1;
(2)由直线l:y=mx+n与圆x2+y2=3相切,
可得$\frac{|n|}{\sqrt{1+{m}^{2}}}$=$\sqrt{3}$,即为n2=3+3m2,
令x=1可得y=±$\sqrt{3(1-\frac{1}{4})}$=±$\frac{3}{2}$,即|CD|=3,
设M(x1,y1),N(x2,y2),
由$\left\{\begin{array}{l}{y=mx+n}\\{3{x}^{2}+4{y}^{2}=12}\end{array}\right.$可得(3+4m2)x2+8mnx+4n2-12=0,
即有△=64m2n2-4(3+4m2)(4n2-12)>0,化为3+4m2>n2,
可得3+3m2<3+4m2,即有m≠0,
x1+x2=-$\frac{8mn}{3+4{m}^{2}}$,x1x2=$\frac{4{n}^{2}-12}{3+4{m}^{2}}$,
|x1-x2|=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{\frac{64{m}^{2}{n}^{2}}{(4{m}^{2}+3)^{2}}-\frac{4(4{n}^{2}-12)}{3+4{m}^{2}}}$=$\frac{4\sqrt{3}|m|}{3+4{m}^{2}}$,
则四边形CMDN的面积S=$\frac{1}{2}$|CD|•|x1-x2|=$\frac{1}{2}$•3•$\frac{4\sqrt{3}|m|}{3+4{m}^{2}}$
=$\frac{6\sqrt{3}}{\frac{3}{|m|}+4|m|}$≤$\frac{6\sqrt{3}}{2\sqrt{12}}$=$\frac{3}{2}$.
当且仅当4|m|=$\frac{3}{|m|}$,即m=±$\frac{\sqrt{3}}{2}$,取得最大值,此时n2=3+$\frac{9}{4}$,
可得n=±$\frac{\sqrt{21}}{2}$,检验可得直线y=$\frac{\sqrt{3}}{2}$x-$\frac{\sqrt{21}}{2}$和y=-$\frac{\sqrt{3}}{2}$x+$\frac{\sqrt{21}}{2}$,符合题意.
(直线y=$\frac{\sqrt{3}}{2}$x+$\frac{\sqrt{21}}{2}$和y=-$\frac{\sqrt{3}}{2}$x-$\frac{\sqrt{21}}{2}$与椭圆交于M,N不在CD的两侧,舍去).
点评 本题考查椭圆方程的求法,注意运用椭圆的定义和三点共线取得最小值,考查四边形面积的最大值及直线方程的求法,注意联立直线方程和椭圆方程,运用韦达定理和判别式大于0,同时考查基本不等式的运用:求最值,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 若x>1,则x2≤1 | B. | 若x2≤1,则x≤1 | C. | 若x≤1,则x2≤1 | D. | 若x<1,则x2<1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{9}{4}$ | C. | 3 | D. | 3+2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题p∨q是假命题 | B. | 命题p∧q是真命题 | ||
| C. | 命题p∧(¬q)是真命题 | D. | 命题p∨(¬q)是假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{9}{5}$ | B. | -$\frac{12}{5}$ | C. | $\frac{12}{5}$ | D. | $\frac{9}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0” | |
| B. | 若a∈R,则“a=2”是“(a-1)(a-2)=0”的充分且不必要条件 | |
| C. | 对于命题p:?x0∈R,使得x02+x0+1<0,则¬p:?x∈R,则x2+x+1≥0 | |
| D. | 命题“若am2<bm2,则a<b”的逆命题是真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{100}{101}$ | B. | $\frac{99}{100}$ | C. | $\frac{101}{100}$ | D. | $\frac{200}{101}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 7 | C. | 1 | D. | -7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com