
分析 (Ⅰ)将x=2代入原函数和导函数,求出切点坐标和切线斜率,得到切线的点斜式方程,将(0,-1)代入,可求a的值;
(Ⅱ)若证:当a≤-1时,不等式f(x)•lnx≥0在(0,1)∪(1,+∞)上恒成立.只需证:(x-1)(ex-1)-ax≥0在(0,+∞)恒成立,设g(x)=(x-1)(ex-1)-ax,x∈[0,+∞),利用导数法求其最值后,可得结论.
解答 解:(Ⅰ)解由x-1≠0得:函数f(x)=ex-1-$\frac{ax}{x-1}$的定义域为x∈(-∞,1)∪(1,+∞),
f(2)=e2-1-2a,$f'(x)={e^x}-\frac{{a({x-1})-ax}}{{{{({x-1})}^2}}}={e^x}+\frac{a}{{{{({x-1})}^2}}}$,
∴f'(2)=e2+a,
∴曲线y=f(x)在(2,f(2))处的切线y-(e2-1-2a)=(e2+a)(x-2)
将(0,-1)代入,得-1-(e2-1-2a)=-2e2-2a,
解得:$a=-\frac{{e}^{2}}{4}$
证明:(Ⅱ)$f(x)•lnx=({{e^x}-1-\frac{ax}{x-1}})•lnx$
若证:当a≤-1时,不等式f(x)•lnx≥0在(0,1)∪(1,+∞)上恒成立.
只需证:$\frac{1}{x-1}•lnx•[{({x-1})({{e^x}-1})-ax}]≥0$在(0,1)∪(1,+∞)上恒成立,
∵x∈(0,1)∪(1,+∞)时,$\frac{1}{x-1}•lnx>0$恒成立,
∴只需证:(x-1)(ex-1)-ax≥0在(0,+∞)恒成立
设g(x)=(x-1)(ex-1)-ax,x∈[0,+∞)
∵g(0)=0恒成立
∴只需证:g(x)≥0在[0,+∞)恒成立
∵g'(x)=x•ex-1-a,
g''(x)=(x+1)•ex>0恒成立,
∴g'(x)单调递增,
∴g'(x)≥g'(0)=-1-a≥0
∴g(x)单调递增,
∴g(x)≥g(0)=0
∴g(x)≥0在[0,+∞)恒成立
即$f(x)•lnx=\frac{1}{x-1}•lnx•g(x)≥0$在(0,1)∪(1,+∞)上恒成立.
点评 本题考查的知识点是利用导数求闭区间上函数的最值,利用导数研究曲线上过某点的切线方程,难度中档.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$\frac{1}{x-1}$ | B. | y=2x-1 | C. | y=$\sqrt{x-1}$ | D. | y=ln(x-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
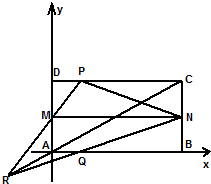 如图所示,已知四边形ABCD是矩形,M,N分别是AD,BC的中点,P是CD上一点,Q是AB上一点,PM与QN交于R,A是原点,B(2,0),C(2,1),D(0,1),P(t,1),Q(t,0),
如图所示,已知四边形ABCD是矩形,M,N分别是AD,BC的中点,P是CD上一点,Q是AB上一点,PM与QN交于R,A是原点,B(2,0),C(2,1),D(0,1),P(t,1),Q(t,0),查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com