
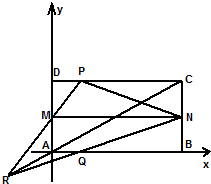
 如图所示,已知四边形ABCD是矩形,M,N分别是AD,BC的中点,P是CD上一点,Q是AB上一点,PM与QN交于R,A是原点,B(2,0),C(2,1),D(0,1),P(t,1),Q(t,0),
如图所示,已知四边形ABCD是矩形,M,N分别是AD,BC的中点,P是CD上一点,Q是AB上一点,PM与QN交于R,A是原点,B(2,0),C(2,1),D(0,1),P(t,1),Q(t,0),分析 (1)求出相关向量,利用 $\overrightarrow{MP}⊥\overrightarrow{NP}$?$\overrightarrow{MP}$•$\overrightarrow{NP}$=0,求解即可.
(2)R,M,P三点共线,设出$\overrightarrow{MR}$=x$\overrightarrow{MP}$,R,N,Q三点共线,可设$\overrightarrow{NR}$=y$\overrightarrow{NQ}$,然后列出方程组求解证明即可.
解答 (1)解:$\overrightarrow{MP}$=(t,1)-(0,$\frac{1}{2}$)=(t,$\frac{1}{2}$),$\overrightarrow{NP}$=(t,1)-(2,$\frac{1}{2}$)=(t-2,$\frac{1}{2}$)…(3分)
$\overrightarrow{MP}$•$\overrightarrow{NP}$=0,所以t(t-2)+$\frac{1}{4}$=0,t=1±$\frac{\sqrt{3}}{2}$…(6分)
(2)证明:R,M,P三点共线,可设$\overrightarrow{MR}$=x$\overrightarrow{MP}$,所以 $\overrightarrow{AR}$=$\overrightarrow{AM}$+x $\overrightarrow{MP}$=(xt,$\frac{1}{2}$(1+x))
R,N,Q三点共线,可设$\overrightarrow{NR}$=y$\overrightarrow{NQ}$,
所以$\overrightarrow{AR}$=$\overrightarrow{AN}$+y$\overrightarrow{NQ}$=(2+y(t-2),$\frac{1}{2}$(1-y))…(10分)
根据平面向量的基本定理得:$\left\{\begin{array}{l}{xt=2+y(t-2)}\\{\frac{1}{2}(1+x)=\frac{1}{2}(1-y)}\end{array}\right.$,解得:x=$\frac{1}{t-1}$,y=-$\frac{1}{t-1}$所.
以$\overrightarrow{AR}$=($\frac{t}{t-1}$,$\frac{t}{2(t-1)}$ )=$\frac{t}{2(t-1)}$ (2,1)=$\frac{t}{2(t-1)}$ $\overrightarrow{AC}$.…(15分)
点评 本题考查向量的应用,向量共线与垂直条件的应用,考查计算能力.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?n∈N*,2n2+5n+2能被2整除是真命题 | |
| B. | ?n∈N*,2n2+5n+2不能被2整除是真命题 | |
| C. | ?n∈N*,2n2+5n+2不能被2整除是真命题 | |
| D. | ?n∈N*,2n2+5n+2能被2整除是假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1<x<2} | B. | {x|-1≤x<2} | C. | {x|x≥-1} | D. | {x|x<2} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
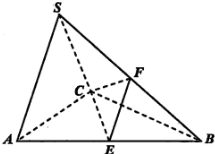 在三棱锥S-ABC中,△ABC是边长为2的正三角形,平面SAC⊥平面ABC,$SA=SC=\sqrt{3}$,E,F分别为AB,SB的中点.
在三棱锥S-ABC中,△ABC是边长为2的正三角形,平面SAC⊥平面ABC,$SA=SC=\sqrt{3}$,E,F分别为AB,SB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com