练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

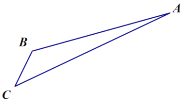
    【题目】如图，游客从某旅游景区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C，另一种是先从A沿索道乘缆车到B，然后从B沿直线步行到C.现有甲、乙两位游客从A处下山，甲沿AC匀速步行，速度为.在甲出发后，乙从A乘缆车到B，在B处停留后，再从B匀速步行到C.假设缆车匀速直线运动的速度为，山路AC长为，经测量，，.当乙出发________分钟时，乙在缆车上与甲的距离最短.

    【答案】

    【解析】

    在中，根据，，由正弦定理求得，得到在AB段时间的范围，假设乙出发t分钟时，甲，乙两游客距离为d，此时，甲行走了，乙距离A处，由余弦定理得，再利用二次函数求解.

    在中，因为，，

    所以，，

    从而，.

    由正弦定理得：，得，

    所以在AB段的时间，即，

    假设乙出发t分钟时，甲，乙两游客距离为d，此时，甲行走了，乙距离A处，

    由余弦定理得，

    ，

    ，

    因为，

    故时，甲，乙两游客的距离最短.

    故答案为：

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】函数的一段图象如图所示.

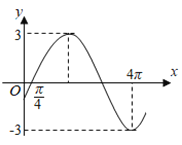
    （1）求的解析式；

    （2）求的单调减区间，并指出的最大值及取到最大值时的集合；

    （3）把的图象向右至少平移多少个单位，才能使得到的图象对应的函数为偶函数？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2017年“双节”期间，高速公路车辆较多．某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查，将他们在某段高速公路的车速分成六段： ， ， ， ， ， 后得到如图的频率分布直方图．

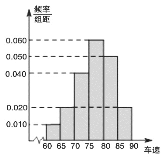
    （1）调查公司在采样中，用到的是什么抽样方法？

    （2）求这40辆小型车辆车速的众数、中位数及平均数的估计值；

    （3）若从车速在的车辆中任抽取2辆，求车速在的车辆至少有一辆的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】△ABC的内角A，B，C的对边分别为a，b，c，已知△ABC的面积为

    （1）求sinBsinC;

    （2）若6cosBcosC=1，a=3，求△ABC的周长.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了让贫困地区的孩子们过一个温暖的冬天，某校阳光志愿者社团组织“这个冬天不再冷”冬衣募捐活动，共有50名志愿者参与.志愿者的工作内容有两项：①到各班做宣传，倡议同学们积极捐献冬衣；②整理、打包募捐上来的衣物.每位志愿者根据自身实际情况，只参与其中的某一项工作.相关统计数据如下表所示：

    （1）如果用分层抽样的方法从参与两项工作的志愿者中抽取5人，再从这5人中选2人，那么“至少有1人是参与班级宣传的志愿者”的概率是多少？

    （2）若参与班级宣传的志愿者中有12名男生，8名女生，从中选出2名志愿者，用表示所选志愿者中的女生人数，写出随机变量的分布列及数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】过平面直角坐标系中的点P（4-3a，）（a∈R）作圆x2+y2=1的两条切线PA，PB，切点分别为A，B，则数量积的最小值为（　　）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某中心接到其正东、正西、正北方向三个观测点的报告：正西、正北两个观测点同时听到了一声巨响，正东观测点听到的时间比其它两观测点晚4.已知各观测点到该中心的距离是1020.则该巨响发生在接报中心的（ ）处.（假定当时声音传播的速度为340，相关各点均在同一平面上）

    A. 西偏北方向，距离 B. 东偏南方向，距离

    C. 西偏北方向，距离 D. 东偏南方向，距离

    查看答案和解析>>

    科目：高中数学 来源： 题型：

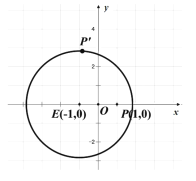
    【题目】如图，一张坐标纸上一已作出圆及点，折叠此纸片，使与圆周上某点重合，每次折叠都会留下折痕，设折痕与直线的交点为，令点的轨迹为.

    （1）求轨迹的方程；

    （2）若直线与轨迹交于两个不同的点，且直线与以为直径的圆相切，若，求的面积的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，以坐标原点为极点， 轴正半轴为极轴，取相同的长度单位建立极坐标系，曲线的极坐标方程为.

    (1)求曲线的直角坐标方程；

    (2)在平面直角坐标系中，将曲线的纵坐标不变，横坐标变为原来的2倍，得到曲线，过点作直线，交曲线于两点，若，求直线的斜率.

    查看答案和解析>>

    同步练习册答案