
分析 (1)由已知得到关于a,b,c的关系式,结合隐含条件即可求得椭圆的离心率;
(2)由(1)可得椭圆方程为$\frac{{x}^{2}}{2{c}^{2}}+\frac{{y}^{2}}{{c}^{2}}=1$,设P(x0,y0),由题意得$\overrightarrow{{F}_{1}P}•\overrightarrow{{F}_{1}B}=0$,再由P在椭圆上把P的坐标用含有c的代数式表示,求出圆心坐标,设出经过原点O与圆C相切的直线l的方程,由点到直线的距离公式求得k,则直线方程可求.
解答 解:(1)由2AB=$\sqrt{3}$F1F2,得$2\sqrt{{a}^{2}+{b}^{2}}=\sqrt{3}•2c$,∴a2+b2=3c2,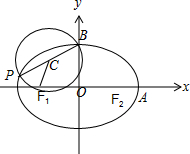
则a2+(a2-c2)=3c2,整理得a2=2c2,∴c=$\frac{\sqrt{2}}{2}a$,即e=$\frac{c}{a}=\frac{\sqrt{2}}{2}$;
(2)由(1)知,a2=2c2,b2=c2,
故椭圆方程为$\frac{{x}^{2}}{2{c}^{2}}+\frac{{y}^{2}}{{c}^{2}}=1$.
设P(x0,y0),由题意得,$\overrightarrow{{F}_{1}P}•\overrightarrow{{F}_{1}B}=0$,
又F1(-c,0),B(0,c),∴$\overrightarrow{{F}_{1}P}=({x}_{0}+c,{y}_{0})$,$\overrightarrow{{F}_{1}B}=(c,c)$,
∴(x0+c)c+y0c=0,
又c>0,∴x0+y0+c=0,①
又$\frac{{{x}_{0}}^{2}}{2{c}^{2}}+\frac{{{y}_{0}}^{2}}{{c}^{2}}=1$,②
由①②,得$3{{x}_{0}}^{2}+4c{x}_{0}=0$,得${x}_{0}=-\frac{4}{3}c$,则${y}_{0}=\frac{c}{3}$.
∴P($-\frac{4}{3}c,\frac{c}{3}$),从而可得圆心C($-\frac{2}{3}c,\frac{2}{3}c$),
∴半径r=|CF1|=$\sqrt{(-\frac{2}{3}c+c)^{2}+(\frac{2c}{3})^{2}}=\frac{\sqrt{5}}{3}c$,
设直线l的方程为y=kx,则
d=$\frac{|-\frac{2}{3}c•k-\frac{2c}{3}|}{\sqrt{1+{k}^{2}}}=\frac{\sqrt{5}}{3}c$,即k2-8k+1=0.
解得k=4$±\sqrt{15}$.
∴直线l的方程为y=($4±\sqrt{15}$)x.
点评 本题考查椭圆的简单性质,考查直线与圆锥曲线位置关系的应用,考查计算能力,是中档题.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 个人家庭用车消费汽油费 | ≤880元/月 | 880~920元/月 | 920~940元/月 | ≥940元/月 |
| 税 率 | 不纳税 | 0.01 | 0.02 | 0.05 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
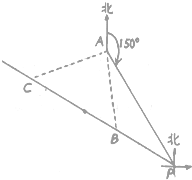 海滨某城市A附近海面上有一台风,在城市A测得该台风中心位于方位角150°、距离400km的海面P处,并正以70km/h的速度沿北偏西60°的方向移动,如果台风侵袭的范围是半径为250km的圆形区域.
海滨某城市A附近海面上有一台风,在城市A测得该台风中心位于方位角150°、距离400km的海面P处,并正以70km/h的速度沿北偏西60°的方向移动,如果台风侵袭的范围是半径为250km的圆形区域.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com