练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3．抛物线y2=4x上一点P和焦点F的距离等于5，则点P的坐标是（4，4），（4，-4）．

    分析 设P（m，n），求出抛物线的准线方程，运用抛物线的定义可得m+1=5，即可解得m，再由抛物线方程，可得n，进而得到P的坐标．

    解答 解：设P（m，n），
    由于抛物线y2=4x的准线为x=-1，
    则由定义可得|PF|=m+1=5，
    解得m=4，
    则n2=16，解得n=-4和4．
    即有P（4，4）或（4，-4）．
    故答案为：（4，4），（4，-4）．

    点评 本题考查抛物线的定义、方程和性质，主要考查抛物线的准线方程的运用，运用定义是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2017届山东潍坊临朐县高三10月月考数学（文）试卷（解析版） 题型：解答题

    设函数为奇函数，为常数.

    （Ⅰ）求实数的值；

    （Ⅱ）讨论函数的单调性，并写出单调区间；

    查看答案和解析>>

    科目：高中数学 来源：2017届江西省红色七校高三上学期联考一数学（理）试卷（解析版） 题型：解答题

    已知数列的前项和，，数列满足.

    （Ⅰ）求数列的通项公式；

    （Ⅱ）是否存在正实数，使得为等比数列？并说明理由.

    查看答案和解析>>

    科目：高中数学 来源：2017届江西省红色七校高三上学期联考一数学（理）试卷（解析版） 题型：选择题

    已知集合则（ ）

    A． B． C． D．

    查看答案和解析>>

    科目：高中数学 来源：2017届河北正定中学高三上月考一数学（理）试卷（解析版） 题型：解答题

    在一次篮球定点投篮训练中，规定每人最多投3次，在处每投进一球得3分；在处每投进一球得2分．如果前两次得分之和超过3分就停止投篮；否则投第三次．某同学在处的投中率，在处的投中率为，该同学选择先在处投第一球，以后都在处投，且每次投篮都互不影响，用表示该同学投篮训练结束后所得的总分，其分布列为：

    0

    2

    3

    4

    5

    0.03

    （1）求的值；

    （2）求随机变量的数学期望；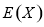

    （3）试比较该同学选择上述方式投篮得分超过3分与选择都在处投篮得分超过3分的概率的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．下列说法正确的是③（填序号）．
    ①有一个面是多边形，其余各面都是三角形，由这些面所围成的几何体是棱锥；
    ②用一个平面去截棱锥，底面与截面之间部分所围成的几何体叫做棱台；
    ③三棱锥的任何一个面都可看作底面．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．已知函数f（x）=2x+$\frac{4}{x}$-1，求f（x）的极值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．数列{an}中，a1=1，a2=3，an2-an-1•an+1=（-1）n-1（n≥2），那么a4=33．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．已知函数f（x）=$\left\{\begin{array}{l}{x+3，x＞a}\\{{x}^{2}+6x+3，x≤a}\end{array}\right.$函数g（x）=f（x）-2x恰有三个不同的零点，则实数a的取值范围是（　　）
    A．[-1，3）B．[-3，-1]C．[-3，3）D．[-1，1）

    查看答案和解析>>

    同步练习册答案