
【题目】如图,在四棱柱![]() 中,点
中,点![]() 和
和![]() 分别为
分别为![]() 和
和![]() 的中点,侧棱
的中点,侧棱![]() 底面
底面![]()
![]() .
.

(1)求证:![]() //平面
//平面![]() ;
;
(2)求二面角![]() 的正弦值
的正弦值
【答案】(1)证明见解析(2)![]()
【解析】
(1)根据题意,以![]() 为坐标原点建立空间直角坐标系,写出各个点的坐标,可通过证明
为坐标原点建立空间直角坐标系,写出各个点的坐标,可通过证明![]() 与平面
与平面![]() 的法向量垂直,来证明
的法向量垂直,来证明![]() //平面
//平面![]() .
.
(2)根据(1)中建立的平面直角坐标系,分别求得平面![]() 的法向量
的法向量![]() 与平面
与平面![]() 的法向量
的法向量![]() ,即可求得两个平面夹角的余弦值,结合同角三角函数关系式即可求得二面角
,即可求得两个平面夹角的余弦值,结合同角三角函数关系式即可求得二面角![]() 的正弦值.
的正弦值.
(1)证明:根据题意,以![]() 为坐标原点,
为坐标原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴建立如下图所示的空间直角坐标系:
轴建立如下图所示的空间直角坐标系:
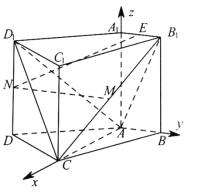
点![]() 和
和![]() 分别为
分别为![]() 和
和![]() 的中点,
的中点, ![]() ,
,![]()
则![]() ,则
,则![]()
![]() ,则
,则![]()
所以![]()
依题意可知![]() 为平面
为平面![]() 的一个法向量
的一个法向量
而![]()
所以![]()
又因为直线![]() 平面
平面![]()
所以![]() 平面
平面![]()
(2)![]()
设![]() 为平面
为平面![]() 的法向量,
的法向量,
则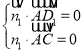 ,即
,即![]()
不妨设![]() ,可得
,可得![]()
设![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
则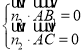 ,又
,又![]() ,得
,得![]()
不妨设![]() ,可得
,可得![]()
因此有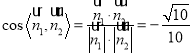 ,
,
于是![]()
所以二面角![]() 的正弦值为
的正弦值为![]()


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】随着“互联网+交通”模式的迅猛发展,“共享助力单车”在很多城市相继出现.某“共享助力单车”运营公司为了解某地区用户对该公司所提供的服务的满意度,随机调查了100名用户,得到用户的满意度评分(满分10分),现将评分分为5组,如下表:
组别 | 一 | 二 | 三 | 四 | 五 |
满意度评分 | [0,2) | [2,4) | [4,6) | [6,8) | [8,10] |
频数 | 5 | 10 | a | 32 | 16 |
频率 | 0.05 | b | 0.37 | c | 0.16 |
(1)求表格中的a,b,c的值;
(2)估计用户的满意度评分的平均数;
(3)若从这100名用户中随机抽取25人,估计满意度评分低于6分的人数为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线![]() 的参数方程为
的参数方程为 (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与曲线C交于
与曲线C交于![]() 两点.
两点.
(1)求直线![]() 的普通方程和曲线C的直角坐标方程;
的普通方程和曲线C的直角坐标方程;
(2)求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
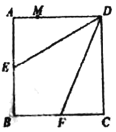
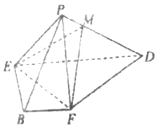
【题目】如图,在正方形![]() 中,点
中,点![]() 是
是![]() 的中点,点
的中点,点![]() 是
是![]() 的中点,将
的中点,将![]() 分别沿
分别沿![]() 折起,使
折起,使![]() 两点重合于
两点重合于![]() ,连接
,连接![]() .
.
(1)求证:![]() ;
;
(2)点![]() 是
是![]() 上一点,若
上一点,若![]() 平面
平面![]() ,则
,则![]() 为何值?并说明理由.
为何值?并说明理由.
(3)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在[29.94,30.06)的零件为优质品.从两个分厂生产的零件中各抽出了500件,量其内径尺寸,得结果如下表:
甲厂:
分组 | [29.86,29.90) | [29.90,29.94) | [29.94,29.98) | [29.98,30.02) | [30.02,30.06) | [30.06,30.10) | [30.10,30.14) |
频数 | 12 | 63 | 86 | 182 | 92 | 61 | 4 |
乙厂:
分组 | [29.86,29.90) | [29.90,29.94) | [29.94,29.98) | [29.98,30.02) | [30.02,30.06) | [30.06,30.10) | [30.10,30.14) |
频数 | 29 | 71 | 85 | 159 | 76 | 62 | 18 |
(1)试分别估计两个分厂生产的零件的优质品率;
(2)由以上统计数据填下面![]() 列联表,并问是否有
列联表,并问是否有![]() 的把握认为“两个分厂生产的零件的质量有差异”.
的把握认为“两个分厂生产的零件的质量有差异”.
甲 厂 | 乙 厂 | 合计 | |
优质品 | |||
非优质品 | |||
合计 |
附: 
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为响应“生产发展、生活富裕、乡风文明、村容整洁、管理民主”的社会主义新农村建设,某自然村将村边一块废弃的扇形荒地(如图)租给蜂农养蜂、产蜜与售蜜.已知扇形AOB中,![]() ,
,![]() 百米),荒地内规划修建两条直路AB,OC,其中点C在弧AB上(C与A,B不重合),在小路AB与OC的交点D处设立售蜜点,图中阴影部分为蜂巢区,空白部分为蜂源植物生长区.设
百米),荒地内规划修建两条直路AB,OC,其中点C在弧AB上(C与A,B不重合),在小路AB与OC的交点D处设立售蜜点,图中阴影部分为蜂巢区,空白部分为蜂源植物生长区.设![]() ,蜂巢区的面积为S(平方百米).
,蜂巢区的面积为S(平方百米).

(1)求S关于![]() 的函数关系式;
的函数关系式;
(2)当![]() 为何值时,蜂巢区的面积S最小,并求此时S的最小值.
为何值时,蜂巢区的面积S最小,并求此时S的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com