
【题目】已知函数![]() (
(![]() 为常数,
为常数,![]() …是自然对数的底数),曲线
…是自然对数的底数),曲线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴平行.
轴平行.
(1)求![]() 的值;
的值;
(2)求函数![]() 的单调区间;
的单调区间;
(3)设![]() ,其中
,其中![]() 为
为![]() 的导函数.证明:对任意
的导函数.证明:对任意![]() ,
,![]() .
.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】第十三届全国人大常委会第十一次会议审议的《固体废物污染环境防治法(修订草案)》中,提出推行生活垃圾分类制度,这是生活垃圾分类首次被纳入国家立法中.为了解某城市居民的垃圾分类意识与政府相关法规宣传普及的关系,对某试点社区抽取![]() 户居民进行调查,得到如下的
户居民进行调查,得到如下的![]() 列联表.
列联表.
分类意识强 | 分类意识弱 | 合计 | |
试点后 |
| ||
试点前 |
| ||
合计 |
|
已知在抽取的![]() 户居民中随机抽取
户居民中随机抽取![]() 户,抽到分类意识强的概率为
户,抽到分类意识强的概率为![]() .
.
(1)请将上面的![]() 列联表补充完整,并判断是否有
列联表补充完整,并判断是否有![]() 的把握认为居民分类意识的强弱与政府宣传普及工作有关?说明你的理由;
的把握认为居民分类意识的强弱与政府宣传普及工作有关?说明你的理由;
(2)已知在试点前分类意识强的![]() 户居民中,有
户居民中,有![]() 户自觉垃圾分类在
户自觉垃圾分类在![]() 年以上,现在从试点前分类意识强的
年以上,现在从试点前分类意识强的![]() 户居民中,随机选出
户居民中,随机选出![]() 户进行自觉垃圾分类年限的调查,记选出自觉垃圾分类年限在
户进行自觉垃圾分类年限的调查,记选出自觉垃圾分类年限在![]() 年以上的户数为
年以上的户数为![]() ,求
,求![]() 分布列及数学期望.
分布列及数学期望.
参考公式: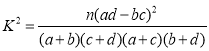 ,其中
,其中![]() .
.
下面的临界值表仅供参考
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某汽车站每天均有3辆开往省城的分为上、中、下等级的客车,某天袁先生准备在该汽车站乘车前往省城办事,但他不知道客车的车况,也不知道发车顺序.为了尽可能乘上上等车,他采取如下策略:先放过一辆,如果第二辆比第一辆好则上第二辆,否则上第三辆.则他乘上上等车的概率为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).以
为参数).以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() ),将曲线
),将曲线![]() 向左平移2个单位长度得到曲线
向左平移2个单位长度得到曲线![]() .
.
(1)求曲线![]() 的普通方程和极坐标方程;
的普通方程和极坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形![]() ,
,![]() 为
为![]() 的中点,将
的中点,将![]() 沿直线
沿直线![]() 翻折成
翻折成![]() ,连接
,连接![]() ,
,![]() 为
为![]() 的中点,则在翻折过程中,下列说法中所有正确的是( )
的中点,则在翻折过程中,下列说法中所有正确的是( )
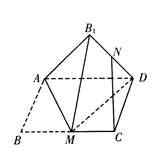
A.存在某个位置,使得![]() B.翻折过程中,
B.翻折过程中,![]() 的长是定值
的长是定值
C.若![]() ,则
,则![]() ;D.若
;D.若![]() ,当三棱锥
,当三棱锥![]() 的体积最大时,三棱锥
的体积最大时,三棱锥![]() 的外接球的表面积是
的外接球的表面积是![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=sin(wx+![]() )(w>0,
)(w>0,![]() <
<![]() )的最小正周期是π,若将该函数的图象向右平移
)的最小正周期是π,若将该函数的图象向右平移![]() 个单位后得到的函数图象关于直线x=
个单位后得到的函数图象关于直线x=![]() 对称,则函数f(x)的解析式为( )
对称,则函数f(x)的解析式为( )
A.f(x)=sin(2x+![]() )B.f(x)=sin(2x-
)B.f(x)=sin(2x-![]() )
)
C.f(x)=sin(2x+![]() )D.f(x)=sin(2x-
)D.f(x)=sin(2x-![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com