
分析 (Ⅰ)原不等式可化为$\left\{{\begin{array}{l}{x<-1}\\{{{(\frac{1}{2})}^x}+4<12}\end{array}}\right.$或 $\left\{{\begin{array}{l}{x≥-1}\\{{x^2}+4x<12}\end{array}}\right.$,解出即可得出.
(Ⅱ)总存在x0∈[-1,1],使得f(x0)=3-a成立,即函数g(x)=ax2+4x+a-3在[-1,1]上有零点.(1)当g(-1)g(1)≤0时,g(x)在[-1,1]上总有零点,(2)当g(-1)g(1)>0时,分为以下两种其中情况$\left\{{\begin{array}{l}{g(-1)>0}\\{g(1)>0}\\{△≥0}\\{-1<-\frac{4}{2a}<1}\end{array}}\right.$或 $\left\{{\begin{array}{l}{g(-1)<0}\\{g(1)<0}\\{△≥0}\\{-1<-\frac{4}{2a}<1}\end{array}}\right.$,解出即可得出.
解答 解:(Ⅰ)原不等式可化为$\left\{{\begin{array}{l}{x<-1}\\{{{(\frac{1}{2})}^x}+4<12}\end{array}}\right.$或 $\left\{{\begin{array}{l}{x≥-1}\\{{x^2}+4x<12}\end{array}}\right.$,
解得-3<x<-1或-1≤x<2,
所以原不等式的解集是{x|-3<x<2}.
(Ⅱ)总存在x0∈[-1,1],使得f(x0)=3-a成立,即函数g(x)=ax2+4x+a-3在[-1,1]上有零点.
(1)当g(-1)g(1)≤0时,g(x)在[-1,1]上总有零点,
所以(2a-7)(2a+1)≤0,即$-\frac{1}{2}≤a≤\frac{7}{2}$,
(2)当g(-1)g(1)>0时,分为以下两种其中情况$\left\{{\begin{array}{l}{g(-1)>0}\\{g(1)>0}\\{△≥0}\\{-1<-\frac{4}{2a}<1}\end{array}}\right.$或 $\left\{{\begin{array}{l}{g(-1)<0}\\{g(1)<0}\\{△≥0}\\{-1<-\frac{4}{2a}<1}\end{array}}\right.$,
解得$\frac{7}{2}<a≤4$或∅.
综上,实数a的取值范围是$[-\frac{1}{2},4]$.
点评 本题考查了二次函数的单调性、不等式的解法,考查了分类讨论方法、推理能力与计算能力,属于中档题.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | 1 | C. | $\frac{5}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
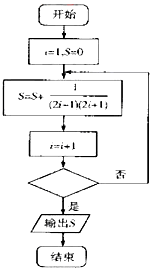
| A. | i>2014 | B. | i>2014 | C. | i>2015 | D. | i>2017 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-2,-1,0,1} | B. | {-1,0,1,2} | C. | {-2,-1,1} | D. | {-2,-1,0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com