
| A. | $\sqrt{5}$ | B. | $\frac{{\sqrt{5}+1}}{2}$ | C. | $\sqrt{5}-1$ | D. | $\sqrt{2}$ |
分析 设抛物线y2=4cx的准线为l,作PQ⊥l于Q,设双曲线的右焦点为F′,P(x,y),利用抛物线的定义、双曲线的渐近线以及直线平行的性质、圆的性质:直径所对的圆周角为直角即可得出所求值.
解答 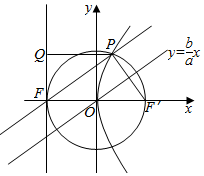 解:如图,设抛物线y2=4cx的准线为l,作PQ⊥l于Q,
解:如图,设抛物线y2=4cx的准线为l,作PQ⊥l于Q,
设双曲线的右焦点为F′,P(x,y).
由题意可知FF′为圆x2+y2=c2的直径,
∴PF′⊥PF,且tan∠PFF′=$\frac{b}{a}$,|FF′|=2c,
满足$\left\{\begin{array}{l}{{y}^{2}=2cx①}\\{{x}^{2}+{y}^{2}={c}^{2}②}\\{\frac{y}{x+c}=\frac{b}{a}③}\end{array}\right.$,
将①代入②得x2+2cx-c2=0,
则x=-c±$\sqrt{2}$c,
即x=($\sqrt{2}$-1)c,(负值舍去),
代入③,即y=$\frac{\sqrt{2}bc}{a}$,
再将y代入①得,$\frac{2{b}^{2}{c}^{2}}{{a}^{2}}$=2($\sqrt{2}$-1)c2,
即为b2=c2-a2=($\sqrt{2}$-1)a2,
由e=$\frac{c}{a}$,可得e2=$\sqrt{2}$.
故选:D.
点评 本题考查双曲线的性质,掌握抛物线的性质、双曲线的渐近线、直线平行的性质、圆的性质是解题的关键.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
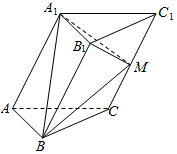 在三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC,M为CC1的中点,∠ABC=90°,AC=A1A,∠A1AC=60°,AB=BC=2.
在三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC,M为CC1的中点,∠ABC=90°,AC=A1A,∠A1AC=60°,AB=BC=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
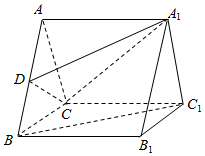 如图,在三棱柱ABC-A1B1C1中,底面△ABC是边长为2的等边三角形.D为AB中点.
如图,在三棱柱ABC-A1B1C1中,底面△ABC是边长为2的等边三角形.D为AB中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{\sqrt{2}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com