Question

18．已知动圆P（P为圆心）经过点N（${\sqrt{3}$，0），并且与M：（x+$\sqrt{3}}$）²+y²=16相切．
（Ⅰ）求点P的轨迹E的方程；
（Ⅱ）经过点A（0，2）的直线l与曲线E相交于点C，D，并且$\overrightarrow{AC}$=$\frac{3}{5}$$\overrightarrow{AD}$，求直线l的方程．

Answer 1

分析 （I）利用圆的相切的性质、椭圆的定义即可得出．
（II）经检验，当直线l⊥x轴时，题目条件不成立，所以直线l存在斜率，设直线l：y=kx+2．设C（x₁，y₁），D（x₂，y₂），直线方程与椭圆方程联立化为：（1+4k²）x²+16kx+12=0．△＞0，利用向量坐标运算性质、一元二次方程的根与系数的关系即可得出．

解答 解：（Ⅰ）设P（x，y）为所求曲线上任意一点，并且⊙P与⊙M相切于点B，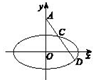
则|PM|+|PN|=|PM|+|PB|=4．
所以点P的轨迹方程为$\frac{x^2}{4}+{y^2}=1$．
（Ⅱ）经检验，当直线l⊥x轴时，题目条件不成立，所以直线l存在斜率，
设直线l：y=kx+2．设C（x₁，y₁），D（x₂，y₂），
则$\left\{\begin{array}{l}\frac{x^2}{4}+{y^2}=1\\ y=kx+2\end{array}\right.⇒（{1+4{k^2}}）{x^2}+16kx+12=0$，
△=（16k）²-4（1+4k²）•12＞0，得${k^2}＞\frac{3}{4}$．
${x_1}+{x_2}=-\frac{16k}{{1+4{k^2}}}$…①，${x_1}{x_2}=\frac{12}{{1+4{k^2}}}$…②，
又由$\overrightarrow{AC}=\frac{3}{5}\overrightarrow{AD}$，得${x_1}=\frac{3}{5}{x_2}$，
将它代入①，②得k²=1，k=±1（满足${k^2}＞\frac{3}{4}$），
所以直线l的斜率为k=±1，所以直线l的方程为y=±x+2．

点评 本题考查了椭圆的定义标准方程及其性质、直线与椭圆相交问题、向量坐标运算性质、一元二次方程的根与系数的关系，考查了推理能力与计算能力，属于难题．