
| A. | 命题“?x∈R,x2-x≤0”的否定是“$?{x_0}∈R,x_0^2-{x_0}≥0$”. | |
| B. | 命题“p∧q为真”是命题“p∨q为真”的必要不充分条件. | |
| C. | “若am2≤bm2,则a≤b”的否命题为真. | |
| D. | 若实数x,y∈[-1,1],则满足x2+y2≥1的概率为$\frac{π}{4}$. |
分析 A,“≤”的否定是“<”;
B,“p∧q为真”是命题“p∨q为真”的充分不必要条件;
C,am2≤bam2⇒m2>0;
D,∵x2+y2≥1的区域是圆的外面的边长为2的正方形内的区域,用面积之比即可.
解答 解:对于A,“≤”的否定是“<”,故错;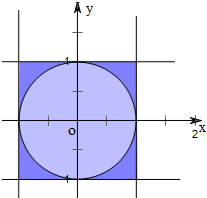
对于B,“p∧q为真”是命题“p∨q为真”的充分不必要条件,故错;
对于C,am2≤bam2⇒m2>0⇒a≤b,故正确;
对于D,如图:∵x2+y2≥1的区域是圆的外面的阴影区域,其面积S=4-π,
∴在区间[-1,1]上任取两个实数x,y,则满足x2+y2≥1的概率为$\frac{4-π}{4}$.故错.
故选:C.
点评 本题考查了命题真假的判定,充要条件的判定及几何概型,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{2}$,$\frac{2}{3}$] | B. | ($\frac{1}{2}$,$\frac{3}{4}$) | C. | ($\frac{3}{4}$,1) | D. | ($\frac{1}{2}$,$\frac{2}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -a>-b | B. | a+c>b+c | C. | $\frac{1}{a}>\frac{1}{b}$ | D. | (-a)2>(-b)2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
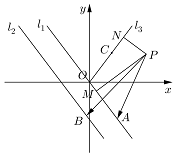 如图,已知直线l1:kx+y=0和直线l2:kx+y+b=0(b>0),射线OC的一个法向量为$\overrightarrow{n_3}$=(-k,1),点O为坐标原点,且k≥0,直线l1和l2之间的距离为2,点A、B分别是直线l1、l2上的动点,P(4,2),PM⊥l1于点M,PN⊥OC于点N;
如图,已知直线l1:kx+y=0和直线l2:kx+y+b=0(b>0),射线OC的一个法向量为$\overrightarrow{n_3}$=(-k,1),点O为坐标原点,且k≥0,直线l1和l2之间的距离为2,点A、B分别是直线l1、l2上的动点,P(4,2),PM⊥l1于点M,PN⊥OC于点N;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com