
分析 (Ⅰ)将原极坐标方程ρcos2θ=4sinθ两边同时乘以ρ,利用极坐标与直角坐标之间的关系即可得出其直角坐标方程;
(Ⅱ)求出直线l的直角坐标方程,代入弦长公式计算即可.
解答 解:(Ⅰ)由ρsin2θ=4cosθ得,ρ2sin2θ=4ρcosθ,
即曲线C的直角坐标方程为y2=4x;
(Ⅱ)∵直线l的参数方程为$\left\{\begin{array}{l}{x=1+t}\\{y=\sqrt{3}t}\end{array}\right.$ (t为参数),
∴直线l的直角坐标方程是:y=$\sqrt{3}$(x-1),
如图示: ,
,
由$\left\{\begin{array}{l}{y=\sqrt{3}(x-1)}\\{{y}^{2}=4x}\end{array}\right.$,得:3x2-10x+3=0,
故x1+x2=$\frac{10}{3}$,x1x2=1,
故|AB|=$\sqrt{1{+k}^{2}}$|x1-x2|=$\sqrt{1+3}$$\sqrt{{(\frac{10}{3})}^{2}-4}$=$\frac{16}{3}$.
点评 本题考查了参数方程、极坐标方程和普通方程的转化,考查弦长公式,是一道中档题.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -$\frac{5}{3}$ | C. | -$\frac{1}{3}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
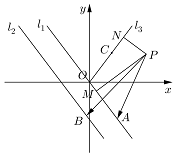 如图,已知直线l1:kx+y=0和直线l2:kx+y+b=0(b>0),射线OC的一个法向量为$\overrightarrow{n_3}$=(-k,1),点O为坐标原点,且k≥0,直线l1和l2之间的距离为2,点A、B分别是直线l1、l2上的动点,P(4,2),PM⊥l1于点M,PN⊥OC于点N;
如图,已知直线l1:kx+y=0和直线l2:kx+y+b=0(b>0),射线OC的一个法向量为$\overrightarrow{n_3}$=(-k,1),点O为坐标原点,且k≥0,直线l1和l2之间的距离为2,点A、B分别是直线l1、l2上的动点,P(4,2),PM⊥l1于点M,PN⊥OC于点N;查看答案和解析>>
科目:高中数学 来源: 题型:选择题
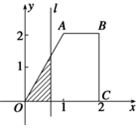 如图,直角梯形OABC中,AB∥OC,|AB|=1,|OC|=|BC|=2,直线l:x=t截此梯形所得位于l左方图形面积为S,则函数S=f(t)的图象大致为图中的( )
如图,直角梯形OABC中,AB∥OC,|AB|=1,|OC|=|BC|=2,直线l:x=t截此梯形所得位于l左方图形面积为S,则函数S=f(t)的图象大致为图中的( )| A. |  | B. | 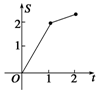 | C. |  | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$\frac{1}{x}$ | B. | y=(x-1)2 | C. | y=2-x | D. | y=log2(x+2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com