
 如图,抛物线C:y2=2px的焦点为F,抛物线上一定点Q(1,2).
如图,抛物线C:y2=2px的焦点为F,抛物线上一定点Q(1,2).分析 (1)把Q(1,2)代入y2=2px,得2p=4,即可求抛物线C的方程及准线l的方程;
(2)把直线AB的方程y=k(x-1),代入抛物线方程y2=4x,并整理,求出k1+k2,k3,即可得出结论.
解答 解:(1)把Q(1,2)代入y2=2px,得2p=4,所以抛物线方程为y2=4x,
准线l的方程为x=-1.
(2)由条件可设直线AB的方程为y=k(x-1),k≠0.
由抛物线准线l:x=-1,可知M(-1,-2k),又Q(1,2),所以${k_3}=\frac{2+2k}{1+1}=k+1$,
把直线AB的方程y=k(x-1),代入抛物线方程y2=4x,并整理,可得k2x2-2(k2+2)x+k2=0,设A(x1,y1),B(x2,y2),则${x_1}+{x_2}=\frac{{2{k^2}+4}}{k^2},{x_1}{x_2}=1$,
又Q(1,2),故${k_1}=\frac{{2-{y_1}}}{{1-{x_1}}},{k_2}=\frac{{2-{y_2}}}{{1-{x_2}}}$.因为A,F,B三点共线,所以kAF=kBF=k,
即$\frac{y_1}{{{x_1}-1}}=\frac{y_2}{{{x_2}-1}}=k$,
所以${k_1}+{k_2}=\frac{{2-{y_1}}}{{1-{x_1}}}+\frac{{2-{y_2}}}{{1-{x_2}}}=\frac{{2k{x_1}{x_2}-({2k+2})({{x_1}+{x_2}})+2k+4}}{{{x_1}{x_2}-({{x_1}+{x_2}})+1}}=2({k+1})$,
即存在常数λ=2,使得k1+k2=2k3成立.
点评 本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与抛物线的相关知识,解题时要注意合理地进行等价转化.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
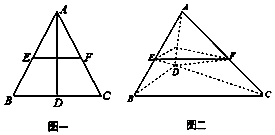 如图一,在边长为2的等边三角形ABC中,D、E、F分别是BC、AB、AC的中点,将△ABD沿AD折起,得到如图二所示的三棱锥A-BCD,其中$BC=\sqrt{2}$.
如图一,在边长为2的等边三角形ABC中,D、E、F分别是BC、AB、AC的中点,将△ABD沿AD折起,得到如图二所示的三棱锥A-BCD,其中$BC=\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,点P为圆E:(x-1)2+y2=r2(r>1)与x轴的左交点,过点P作弦PQ,使PQ与y轴交于PQ的中点D.
如图,点P为圆E:(x-1)2+y2=r2(r>1)与x轴的左交点,过点P作弦PQ,使PQ与y轴交于PQ的中点D.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30 | B. | 25 | C. | 20 | D. | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com