
【题目】设![]() 是数列
是数列![]() 的前
的前![]() 项和,对任意
项和,对任意![]() 都有
都有![]() 成立(其中
成立(其中![]() 是常数).
是常数).
(1)当![]() 时,求
时,求![]() :
:
(2)当![]() 时,
时,
①若![]() ,求数列
,求数列![]() 的通项公式:
的通项公式:
②设数列![]() 中任意(不同)两项之和仍是该数列中的一项,则称该数列是“
中任意(不同)两项之和仍是该数列中的一项,则称该数列是“![]() 数列”,如果
数列”,如果![]() ,试问:是否存在数列
,试问:是否存在数列![]() 为“
为“![]() 数列”,使得对任意
数列”,使得对任意![]() ,都有
,都有![]() ,且
,且![]() ,若存在,求数列
,若存在,求数列![]() 的首项
的首项![]() 的所有取值构成的集合;若不存在.说明理由.
的所有取值构成的集合;若不存在.说明理由.
【答案】(1)![]() (2)①
(2)①![]() ②存在,首项
②存在,首项![]() 所有取值构成的集合为
所有取值构成的集合为![]() 。
。
【解析】
(1)当![]() 时,得到
时,得到![]() ,进而得到
,进而得到![]() ,两式作差,得到数列
,两式作差,得到数列![]() 为等比数列,即可求解.
为等比数列,即可求解.
(2)①![]() 时,
时,![]() ,进而得到
,进而得到![]() ,两式作差,得到数列
,两式作差,得到数列![]() 为等差数列,即可求解.
为等差数列,即可求解.
②确定数列![]() 的通项,利用
的通项,利用![]() 是“
是“![]() 数列”,得到
数列”,得到![]() 是偶数,从而可得
是偶数,从而可得![]() ,再利用条件,验证,即可求解数列
,再利用条件,验证,即可求解数列![]() 的首项的所有取值.
的首项的所有取值.
(1)由题意,当![]() 时,得到
时,得到![]() ,
,
用![]() 代替
代替![]() ,可得
,可得![]() ,
,
两式相减,可得![]() ,即
,即![]() ,即
,即![]() ,
,
令![]() ,可得
,可得![]() ,解答
,解答![]() ,
,
所以数列![]() 是以1为首项,公比为3的等比数列,
是以1为首项,公比为3的等比数列,
所以![]() .
.
(2)①当![]() 时,
时,![]() ,
,
用![]() 代替
代替![]() ,可得
,可得![]() ,
,
两式相减可得![]() ,
,
用![]() 代替
代替![]() ,可得
,可得![]() ,
,
两式相减,可得![]() ,即
,即![]() ,
,
即![]() ,所以数列
,所以数列![]() 为等差数列,
为等差数列,
因为![]() ,可得
,可得![]() ,
,
又由![]() ,解得
,解得![]()
所以数列![]() 的通项公式为
的通项公式为![]() .
.
②由①知数列![]() 是等差数列,因为
是等差数列,因为![]() ,所以
,所以![]() ,
,
又由![]() 是“封闭数列”,可得:
是“封闭数列”,可得:
对任意![]() ,必存在
,必存在![]() ,使得
,使得![]() ,
,
解得![]() ,所以
,所以![]() 为偶数,
为偶数,
又由已知![]() ,可得
,可得![]() ,所以
,所以![]() ,
,
(i)当![]() 时,
时,![]() ,
,
对于任意![]() ,都有
,都有![]() ,
,
(ii)当![]() 时,
时,![]() ,则
,则![]() ,
,
则![]() ,
,
取![]() ,则
,则![]() ,不合题意;
,不合题意;
当![]() 时,
时,![]() ,则
,则![]() ,
,
则![]() ,符合题意;
,符合题意;
当![]() 时,
时,![]() ,则
,则![]() ,
,
所以![]() ,
,
又由![]() ,
,
所以![]() 或
或![]() 或
或![]() 或
或![]() ,
,
所以首项![]() 所有取值构成的集合为
所有取值构成的集合为![]() .
.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:
【题目】为了丰富学生活动,在体育课上,体育教师设计了一个游戏,让甲、乙、丙三人各抓住橡皮带的一端,甲站在直角![]() 斜边
斜边![]() 的中点
的中点![]() 处,乙站在
处,乙站在![]() 处,丙站在
处,丙站在![]() 处.游戏开始,甲不动,乙、丙分别以
处.游戏开始,甲不动,乙、丙分别以![]() 和
和![]() 的速度同时出发,匀速跑向终点
的速度同时出发,匀速跑向终点![]() 和
和![]() ,运动过程中绷紧的橡皮带围成一个如图所示的
,运动过程中绷紧的橡皮带围成一个如图所示的![]() .(规定:只要有一人跑到终点,游戏就结束,且
.(规定:只要有一人跑到终点,游戏就结束,且![]() ).已知
).已知![]() 长为
长为![]() ,
,![]() 长为
长为![]() ,记经过
,记经过![]() 后
后![]() 的面积为
的面积为![]() .
.
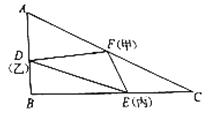
(1)求![]() 关于
关于![]() 的函数表示,并求出
的函数表示,并求出![]() 的取值范围;
的取值范围;
(2)当游戏进行到![]() 时,体育教师宣布停止,求此时
时,体育教师宣布停止,求此时![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省普通高中学业水平考试成绩按人数所占比例依次由高到低分为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五个等级,
五个等级,![]() 等级
等级![]() ,
,![]() 等级
等级![]() ,
,![]() 等级
等级![]() ,
,![]() ,
,![]() 等级共
等级共![]() .其中
.其中![]() 等级为不合格,原则上比例不超过
等级为不合格,原则上比例不超过![]() .该省某校高二年级学生都参加学业水平考试,先从中随机抽取了部分学生的考试成绩进行统计,统计结果如图所示.若该校高二年级共有1000名学生,则估计该年级拿到
.该省某校高二年级学生都参加学业水平考试,先从中随机抽取了部分学生的考试成绩进行统计,统计结果如图所示.若该校高二年级共有1000名学生,则估计该年级拿到![]() 级及以上级别的学生人数有( )
级及以上级别的学生人数有( )
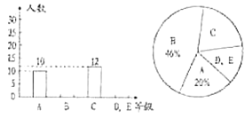
A.45人B.660人C.880人D.900人
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】安徽怀远石榴(Punicagranatum)自古就有“九州之奇树,天下之名果”的美称,今年又喜获丰收.怀远一中数学兴趣小组进行社会调查,了解到某石榴合作社为了实现![]() 万元利润目标,准备制定激励销售人员的奖励方案:在销售利润超过
万元利润目标,准备制定激励销售人员的奖励方案:在销售利润超过![]() 万元时,按销售利润进行奖励,且奖金
万元时,按销售利润进行奖励,且奖金![]() (单位:万元)随销售利润
(单位:万元)随销售利润![]() (单位:万元)的增加而增加,但奖金总数不超过
(单位:万元)的增加而增加,但奖金总数不超过![]() 万元,同时奖金不能超过利润的
万元,同时奖金不能超过利润的![]() .同学们利用函数知识,设计了如下函数模型,其中符合合作社要求的是( )(参考数据:
.同学们利用函数知识,设计了如下函数模型,其中符合合作社要求的是( )(参考数据:![]() )
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某次电影展,有14部参赛影片,组委会分两天在某一影院播映这14部电影,每天7部,其中有2部4D电影要求不在同一天放映,下列不能作为排片方案数的计算式的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动直线![]() 垂直于
垂直于![]() 轴,与椭圆
轴,与椭圆![]() 交于
交于![]() 两点,点
两点,点![]() 在直线
在直线![]() 上,
上,![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,与曲线
,与曲线![]() 相切于点
相切于点![]() ,
,![]() 为坐标原点,求
为坐标原点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com