
(13分) 定义在 上的函数
上的函数 ,如果满足:对任意
,如果满足:对任意 ,存在常数
,存在常数 ,
,
都有 成立,则称
成立,则称 是
是 上的有界函数,其中
上的有界函数,其中 称为函数
称为函数 的上界.
的上界.
已知函数 ;
; 
(I)当 时,求函数
时,求函数 在
在 上的值域,并判断函数
上的值域,并判断函数 在
在 上是否为
上是否为
有界函数,请说明理由;
(Ⅱ)若函数 在
在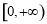 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数 的取值范围;
的取值范围;
(Ⅲ)已知 ,函数
,函数 在
在 上的上界是
上的上界是 ,求
,求 的取值范围.
的取值范围.
(I) 不是有界函数;(Ⅱ)  ;(Ⅲ)
;(Ⅲ)  .
.
【解析】
试题分析:(Ⅰ)将a=1代入f(x)可得 ,利用指数函数的单调性判断出f(x)在
,利用指数函数的单调性判断出f(x)在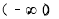 上是单调递减函数,即可求得
上是单调递减函数,即可求得 ,从而得到f(x)的值域,根据有界函数函数的定义,即可判断出f(x)不是有界函数;
,从而得到f(x)的值域,根据有界函数函数的定义,即可判断出f(x)不是有界函数;
(Ⅱ)根据有界函数的定义,可得 在
在 上恒成立,利用参变量分离转化为
上恒成立,利用参变量分离转化为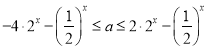 在
在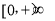 上恒成立,令
上恒成立,令 ,则
,则 ,
,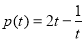 ,问题转化为求h(t)的最大值和p(t)最小值,利用函数单调性的定义,分别判断出函数h(t)和p(t)的单调性,即可求得最值,从容求得a的取值范围.
,问题转化为求h(t)的最大值和p(t)最小值,利用函数单调性的定义,分别判断出函数h(t)和p(t)的单调性,即可求得最值,从容求得a的取值范围.
试题解析:(I)当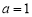 时,
时, ,
,
因为 在
在 上递减,所以
上递减,所以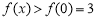 ,即
,即 在
在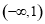 的值域为
的值域为
故不存在常数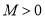 ,使
,使 成立 ,所以函数
成立 ,所以函数 在
在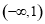 上不是有界函数
上不是有界函数
(Ⅱ)由题意知, 在
在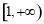 上恒成立.
上恒成立.
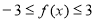 ,
, 
∴  在
在 上恒成立
上恒成立
∴ 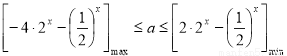
设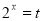 ,
, ,
,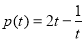 ,由
,由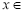
 得 t≥1,
得 t≥1,
(设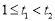 ,
,


所以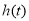 在
在 上递减,
上递减, 在
在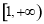 上递增, (单调性不证,不扣分))
上递增, (单调性不证,不扣分))
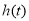 在
在 上的最大值为
上的最大值为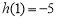 ,
,  在
在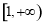 上的最小值为
上的最小值为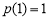
所以实数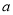 的取值范围为
的取值范围为
(Ⅲ) , ∵ m>0 ,
, ∵ m>0 ,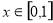 ∴
∴ 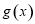 在
在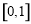 上递减,
上递减,
∴ 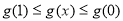 即
即
∵  ,
,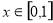 ∴
∴ 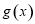 在
在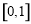 上递增,
上递增,
∴ 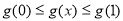 即个
即个
①当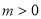 时,
时, ,
, 此时
此时 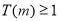
②当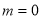 ,即,
,即,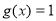 ,
, 此时
此时 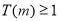 ,
,
③当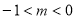 时,
时,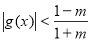 ,此时
,此时 
综上所述:当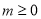 时,
时,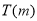 的取值范围是
的取值范围是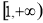 ;
;
当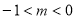 时,
时,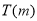 的取值范围是
的取值范围是  .
.
考点:函数恒成立问题;函数最值的应用.


科目:高中数学 来源:2014-2015学年甘肃省天水市高一上学期期中考试数学试卷(解析版) 题型:选择题
若函数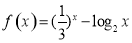 ,实数
,实数 是函数
是函数 的零点,且
的零点,且 ,则
,则 的值( ).
的值( ).
A.恒为正值 B.等于0 C.恒为负值 D.不大于0
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖南省高一上学期第一次月考数学试卷(解析版) 题型:选择题
函数y=f(x)的图象如图所示,观察图象可知函数y=f(x)的定义域、值域分别是( )
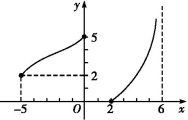
A.[-5, 0]∪[2, 6], [0, 5]
B.[-5, 6], [ 0, +∞)
C.[-5, 0]∪[2, 6), [0, +∞)
D.[-5, +∞), [ 2, 5 ]
查看答案和解析>>
科目:高中数学 来源:2015届吉林省高二下学期期中考试文科数学试卷(解析版) 题型:选择题
在独立性检验中,统计量 有两个临界值:3.841和6.635;当
有两个临界值:3.841和6.635;当
 3.841时,认为两个事件无关,当
3.841时,认为两个事件无关,当 >6.635时,有99%的把握说明两个事件有关.在一项打鼾与患心脏病的调查中,共调查了2000人,经计算的
>6.635时,有99%的把握说明两个事件有关.在一项打鼾与患心脏病的调查中,共调查了2000人,经计算的 =20.87,根据这一数据,认为打鼾与患心脏病之间( )
=20.87,根据这一数据,认为打鼾与患心脏病之间( )
A.认为两者无关 B.约有95%的打鼾者患心脏病
C.有99%的把握认为两者有关 D.约有99%的打鼾者患心脏病
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖南省益阳市高二9月月考文科数学试卷(解析版) 题型:选择题
“ ”是“曲线
”是“曲线 过坐标原点”的( )
过坐标原点”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com