
| A. | f2(f(0))=f(f2(0))?? | B. | f2(f(1))=f(f2(1))?? | C. | f2(f(2))=f(f2(2))?? | D. | f2(f(3))=f(f2(3))?? |
分析 由于函数f(x)=x2-2x-1,p=2,求出f2(x)=$\left\{\begin{array}{l}{{x}^{2}-2x-1,-1≤x≤3}\\{2,x<-1或x>3}\end{array}\right.$,再对选项一一加以判断,即可得到答案.
解答 解:∵函数f(x)=x2-2x-1,p=2,
∴f2(x)=$\left\{\begin{array}{l}{{x}^{2}-2x-1,-1≤x≤3}\\{2,x<-1或x>3}\end{array}\right.$,
∴A.f2[f(0)]=f2(-1)=2,f[f2(0)]=f(-1)=1+2-1=2,故A成立;
B.f2[f(1)]=f2(-2)=2,f[f2(1)]=f(-2)=4+4-1=7,故B不成立;
C.f2[f(2)]=f2(-1)=2,f[f2(2)]=f2(-1)=2,故C成立;
D.f2[f(3)]=f2(2)=-1,f[f2(3)]=f2(2)=-1,故D成立.
故选:B.
点评 本题考查新定义的理解和运用,考查分段函数的运用:求函数值,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
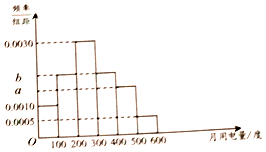 某市为了鼓励市民节约用电,实行“阶梯式”电价,将该市每户居民的月用电量划分为三档,月用电量不超过200度的部分按0.5元/度收费,超过200度但不超过400度的部分按0.8元/度收费,超过400度的部分按1.0元/度收费.
某市为了鼓励市民节约用电,实行“阶梯式”电价,将该市每户居民的月用电量划分为三档,月用电量不超过200度的部分按0.5元/度收费,超过200度但不超过400度的部分按0.8元/度收费,超过400度的部分按1.0元/度收费.查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
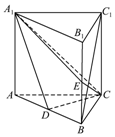 如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=2,AB=2$\sqrt{2}$.
如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=2,AB=2$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4π | B. | 8π | C. | 16π | D. | 20π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{7}+\sqrt{3}}{2}$ | D. | $\sqrt{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图在直角梯形BB1C1C中,∠CC1B1=90°,BB1∥CC1,CC1=B1C1=2BB1=2,D是CC1的中点.四边形AA1C1C可以通过直角梯形BB1C1C以CC1为轴旋转得到,且二面角B1-CC1-A为120°.
如图在直角梯形BB1C1C中,∠CC1B1=90°,BB1∥CC1,CC1=B1C1=2BB1=2,D是CC1的中点.四边形AA1C1C可以通过直角梯形BB1C1C以CC1为轴旋转得到,且二面角B1-CC1-A为120°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数y=f(x)的最小正周期为π | |
| B. | 函数y=f(x)的一个对称中心为$(\frac{7π}{12},\frac{1}{2})$ | |
| C. | 函数y=f(x)在区间$[0,\frac{π}{2}]$上单调递增 | |
| D. | 将函数y=f(x)的图象向右平移$\frac{π}{6}$个单位后,所得图象对应的函数为偶函数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com