
| A. | y=$\frac{1}{x}$ | B. | y=-x2+1 | C. | y=-e-x-ex | D. | y=sinx |
分析 分别利用基本初等函数的函数奇偶性和单调性判断A、B,根据函数奇偶性的定义、导数与函数单调性的关系判断C,由正弦函数的性质判断D.
解答 解:A、y=$\frac{1}{x}$是奇函数,在(-∞,0)、(0,+∞)上是减函数,A不正确;
B.y═-x2+1 在定义域R上是偶函数,不是奇函数,B不正确;
C.y=f(x)=e-x-ex的定义域是R,且f(-x)=ex-e-x=-f(x),则该函数为奇函数,
且y′=-e-x-ex<0,所以该函数在R上是减函数,符合条件,C正确;
D.y=sinx是奇函数,在定义域内不是单调函数,D不正确,
故选C.
点评 本题主要考查函数奇偶性和单调性的判断方法,导数与函数单调性的关系,熟练掌握基本初等函数的奇偶性和单调性是解题的关键.


科目:高中数学 来源: 题型:选择题
| A. | [$\frac{2}{3}$,5] | B. | [$\frac{3}{2}$,11] | C. | [$\frac{1}{5}$,$\frac{2}{3}$] | D. | [$\frac{1}{5}$,$\frac{3}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 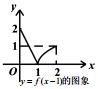 | B. | 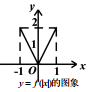 | C. | 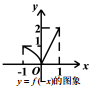 | D. | 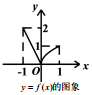 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | -$\sqrt{5}$ | D. | -$\frac{\sqrt{5}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
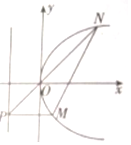 椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左、右焦点分别为F1,F2,离心率e=$\frac{1}{2}$,过F2作x轴垂直的直线交椭圆C于A、B两点,△F1AB的面积为3,抛物线E:y2=2px(p>0)以椭圆C的右焦点F2为焦点.
椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左、右焦点分别为F1,F2,离心率e=$\frac{1}{2}$,过F2作x轴垂直的直线交椭圆C于A、B两点,△F1AB的面积为3,抛物线E:y2=2px(p>0)以椭圆C的右焦点F2为焦点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
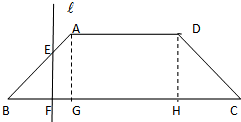 已知底角为45°的等腰梯形ABCD,底边BC长为7cm,腰长为2$\sqrt{2}$cm,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x,试写出左边部分的面积y与x的函数解析式,并画出大致图象.
已知底角为45°的等腰梯形ABCD,底边BC长为7cm,腰长为2$\sqrt{2}$cm,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x,试写出左边部分的面积y与x的函数解析式,并画出大致图象.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com