
分析 据题意即可得到AC⊥BC,从而可分别以CB,CA为x,y轴,建立平面直角坐标系,然后设A(0,a),B(b,0),Q(x,y),从而得到P($\frac{b}{2},\frac{a}{2}$),这样便可得到(x,y)•(b,a)=bx+ay=1,这即可得到(x2+y2)(a2+b2)≥(bx+ay)2,进而得到${x}^{2}+{y}^{2}≥\frac{1}{4}$.可写出直线AB的方程为$\frac{x}{b}+\frac{y}{a}=1$,进而得出$1=(bx+ay)(\frac{x}{b}+\frac{y}{a})$,这便可得到x2+y2≤1,从而便可得出$|\overrightarrow{CQ}|$的取值范围.
解答 解:根据题意知,AC⊥BC,则以CB,CA分别为x,y轴,建立如图所示平面直角坐标系:
设A(0,a),B(b,0),Q(x,y);
|AB|=2,∴a2+b2=4;
$\overrightarrow{CP}=\frac{1}{2}(\overrightarrow{CA}+\overrightarrow{CB})$;
∴P为AB中点,则$P(\frac{b}{2},\frac{a}{2})$;
∴$\overrightarrow{CQ}•\overrightarrow{CP}=(x,y)•(\frac{b}{2},\frac{a}{2})=\frac{bx}{2}+\frac{ay}{2}=\frac{1}{2}$;
∴(x,y)•(b,a)=bx+ay=1;
∴(x2+y2)(a2+b2)≥(bx+ay)2=1;
∴4(x2+y2)≥1;
∴$\sqrt{{x}^{2}+{y}^{2}}≥\frac{1}{2}$;
∴$|\overrightarrow{CQ}|≥\frac{1}{2}$;
又$\frac{x}{b}+\frac{y}{a}=1$;
∴$1=(bx+ay)(\frac{x}{b}+\frac{y}{a})$=${x}^{2}+{y}^{2}+(\frac{b}{a}+\frac{a}{b})xy$;
∵a>0,b>0,x≥0,y≥0;
∴x2+y2≤1;
即$\sqrt{{x}^{2}+{y}^{2}}≤1$;
综上得,$\frac{1}{2}≤|\overrightarrow{CQ}|≤1$;
∴$|\overrightarrow{CQ}|$的取值范围为$[\frac{1}{2},1]$.
故答案为:[$\frac{1}{2}$,1].
点评 考查直角三角形斜边的中线等于斜边的一半,以及通过建立平面直角坐标系,利用坐标解决向量问题的方法,根据点的坐标求向量坐标,中点坐标公式,向量数量积的坐标运算及计算公式,以及直线的斜截式方程.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
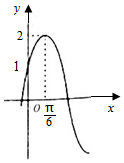
| A. | f(x)=2sin3x | B. | $f(x)=2sin(x+\frac{π}{3})$ | C. | $f(x)=2sin(3x+\frac{π}{6})$ | D. | $f(x)=2sin(2x+\frac{π}{6})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com