
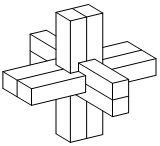
 ³���������й���ͳ��������ߣ���Դ�ڹŴ����彨�����״����î�ṹ��������ά��ƴ�������ڲ��İ����֣����î�ṹ�����ϣ�ʮ�����ԭΪľ�ʽṹ����ۿ�����˿�Ϸ��ʮ�������壬�����£����ң�ǰ����ȫ�Գƣ�������Ͽ��������ȳ�������������ֳ����飬��90���î������������������ĸ�Ϊ4�����������εı߳�Ϊ1�����³�����ı����Ϊ��������
³���������й���ͳ��������ߣ���Դ�ڹŴ����彨�����״����î�ṹ��������ά��ƴ�������ڲ��İ����֣����î�ṹ�����ϣ�ʮ�����ԭΪľ�ʽṹ����ۿ�����˿�Ϸ��ʮ�������壬�����£����ң�ǰ����ȫ�Գƣ�������Ͽ��������ȳ�������������ֳ����飬��90���î������������������ĸ�Ϊ4�����������εı߳�Ϊ1�����³�����ı����Ϊ��������| A�� | 48 | B�� | 60 | C�� | 72 | D�� | 84 |
���� �Ѹ��ӵ�ͼ�α����������ͼͶӰ�ķ���������ã������ü�������һ��ƽ���ϵ�ͶӰ������ͶӰ���������6��ͶӰ������Ӷ����������ı������
��� 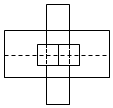 �⣺���ӵ�ͼ�α��������������ͼͶӰ�ķ���������ã�
�⣺���ӵ�ͼ�α��������������ͼͶӰ�ķ���������ã�
��ͼ��ʾ��
ͶӰ���Ϊ4��2+1��2=10��
����6��ͶӰ�����
���Ըü�����ı����Ϊ10��6=60��
��ѡ��B��
���� ���⿼������������ͼͶӰ�ķ������㸴��ͼ�εı������Ӧ�����⣬�ǻ�����Ŀ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
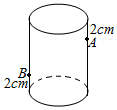 Բ���β�������8cm�������ܳ�Ϊ12cm���ڱھ౭��2cm�ĵ�A����һ�����ǣ�A�����������ڣ�����A�����ڣ��౭��2cm�ĵ�B����һС�森��С���ر����������DZ�ʳһ�٣�����Ҫ������10cm�������Ʊ��ں����С��ijߴ磩
Բ���β�������8cm�������ܳ�Ϊ12cm���ڱھ౭��2cm�ĵ�A����һ�����ǣ�A�����������ڣ�����A�����ڣ��౭��2cm�ĵ�B����һС�森��С���ر����������DZ�ʳһ�٣�����Ҫ������10cm�������Ʊ��ں����С��ijߴ磩�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ij��������۲��ʼλ�ڵ���B�ı�ƫ���ȣ�0���ȣ�$\frac{��}{2}$������������2sin2��$\frac{��}{4}$+�ȣ�-$\sqrt{3}$cos2��=1��AB=AD���ڽӵ��ϼ�����ù۲��A��λ����AD������D�㲹�����ʺ���BD������C��Ͷ���꣬ʹ��C����A��ľ���Ϊ4$\sqrt{3}$km����ù۲��ʻ����Զ����Ϊ8km��
��ͼ��ij��������۲��ʼλ�ڵ���B�ı�ƫ���ȣ�0���ȣ�$\frac{��}{2}$������������2sin2��$\frac{��}{4}$+�ȣ�-$\sqrt{3}$cos2��=1��AB=AD���ڽӵ��ϼ�����ù۲��A��λ����AD������D�㲹�����ʺ���BD������C��Ͷ���꣬ʹ��C����A��ľ���Ϊ4$\sqrt{3}$km����ù۲��ʻ����Զ����Ϊ8km���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{7}$ | B�� | $\frac{2}{7}$ | C�� | $\frac{3}{7}$ | D�� | $\frac{6}{7}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | an=2n | B�� | an=n2+n+2 | ||
| C�� | an=$\left\{\begin{array}{l}{0��n=1}\\{2n-1��n��2}\end{array}\right.$ | D�� | an=$\left\{\begin{array}{l}{0��n=1}\\{2n��n��2}\end{array}\right.$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com