
| A. | an=2n | B. | an=n2+n+2 | ||
| C. | an=$\left\{\begin{array}{l}{0,n=1}\\{2n-1,n≥2}\end{array}\right.$ | D. | an=$\left\{\begin{array}{l}{0,n=1}\\{2n,n≥2}\end{array}\right.$ |
分析 通过牛顿-莱布尼茨公式代入计算可知Sn=n2+n-2,当n≥2时利用an=Sn-Sn-1计算,进而可得结论.
解答 解:∵f(x)=${∫}_{1}^{x}$(2t+1)dt=(t2+t)${|}_{1}^{x}$=x2+x-2,
∴Sn=n2+n-2,
当n≥2时,an=Sn-Sn-1
=(n2+n-2)-[(n-1)2+(n-1)-2]
=2n,
又∵a1=S1=1+1-2=0不满足上式,
∴an=$\left\{\begin{array}{l}{0,}&{n=1}\\{2n,}&{n≥2}\end{array}\right.$,
故选:D.
点评 本题考查数列的通项及前n项和,涉及微积分基本定理、通项与前n项和之间的关系等基础知识,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:选择题
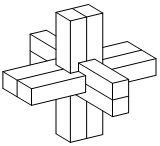 鲁班锁,是中国传统的智力玩具,起源于古代汉族建筑中首创的榫卯结构,这种三维的拼插器具内部的凹凸部分(即榫卯结构)啮合,十分巧妙,原为木质结构,外观看是严丝合缝的十字立方体,其上下,左右,前后完全对称,从外表上看,六根等长的正四棱柱体分成三组,经90度榫卯起来,若正四棱柱体的高为4,底面正方形的边长为1,则该鲁班锁的表面积为( )
鲁班锁,是中国传统的智力玩具,起源于古代汉族建筑中首创的榫卯结构,这种三维的拼插器具内部的凹凸部分(即榫卯结构)啮合,十分巧妙,原为木质结构,外观看是严丝合缝的十字立方体,其上下,左右,前后完全对称,从外表上看,六根等长的正四棱柱体分成三组,经90度榫卯起来,若正四棱柱体的高为4,底面正方形的边长为1,则该鲁班锁的表面积为( )| A. | 48 | B. | 60 | C. | 72 | D. | 84 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 日需求量 | 3 | 4 | 5 | 6 | 7 |
| 频数 | 2 | 3 | 15 | 6 | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1+2i | B. | 1+2i | C. | 1-2i | D. | -1-2i |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充要条件 | B. | 充分但不必要条件 | ||
| C. | 必要但不充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=f(x)的周期为$\frac{π}{2}$ | B. | y=f(x)在[0,$\frac{π}{6}$]上是减函数 | ||
| C. | y=f(x)的图象关于直线x=$\frac{π}{2}$对称 | D. | y=f(x)是偶函数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com