
| A. | 充要条件 | B. | 充分但不必要条件 | ||
| C. | 必要但不充分条件 | D. | 既不充分也不必要条件 |
分析 根据两向量平行与两向量方向相同的关系,结合充分与必要条件的定义,进行判断即可.
解答 解:$\overrightarrow{a}$,$\overrightarrow{b}$均为非零向量,则
“$\overrightarrow{a}$∥$\overrightarrow{b}$”时,“$\overrightarrow{a}$与$\overrightarrow{b}$的方向相同或相反”,充分性不成立;
“$\overrightarrow{a}$与$\overrightarrow{b}$的方向相同”时,“$\overrightarrow{a}$∥$\overrightarrow{b}$”,必要性成立;
所以是必要不充分条件.
故选:C.
点评 本题考查了两向量平行与方向相同的关系,也考查了充分与必要条件的应用问题,是基础题目.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | an=2n | B. | an=n2+n+2 | ||
| C. | an=$\left\{\begin{array}{l}{0,n=1}\\{2n-1,n≥2}\end{array}\right.$ | D. | an=$\left\{\begin{array}{l}{0,n=1}\\{2n,n≥2}\end{array}\right.$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
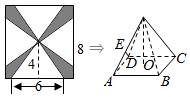 一块边长为8cm的正方形铁片按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角加工成一个正四棱锥(底面是正方形,从顶点向底面作垂线,垂足为底面中心的四棱锥)形容器,O为底面ABCD的中心,E为棱SA的中点,则DE与SC所成角的正切值为$\frac{6\sqrt{2}}{5}$.
一块边长为8cm的正方形铁片按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角加工成一个正四棱锥(底面是正方形,从顶点向底面作垂线,垂足为底面中心的四棱锥)形容器,O为底面ABCD的中心,E为棱SA的中点,则DE与SC所成角的正切值为$\frac{6\sqrt{2}}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{2\sqrt{5}}{5}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | ±$\frac{2\sqrt{5}}{5}$ | D. | $\frac{\sqrt{5}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com