
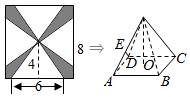
 一块边长为8cm的正方形铁片按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角加工成一个正四棱锥(底面是正方形,从顶点向底面作垂线,垂足为底面中心的四棱锥)形容器,O为底面ABCD的中心,E为棱SA的中点,则DE与SC所成角的正切值为$\frac{6\sqrt{2}}{5}$.
一块边长为8cm的正方形铁片按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角加工成一个正四棱锥(底面是正方形,从顶点向底面作垂线,垂足为底面中心的四棱锥)形容器,O为底面ABCD的中心,E为棱SA的中点,则DE与SC所成角的正切值为$\frac{6\sqrt{2}}{5}$. 分析 以O为原点,OA为x轴,OB为y轴,OS为z轴,建立空间直角坐标系,利用向量法能求出DE与SC所成角的正切值.
解答 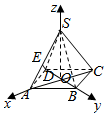 解由已知得正四棱锥S-ABCD中,底面正方形ABCD的边长为6,△SAB的高h=4,
解由已知得正四棱锥S-ABCD中,底面正方形ABCD的边长为6,△SAB的高h=4,
SO=$\sqrt{{4}^{2}+{3}^{2}-(3\sqrt{2})^{2}}$=$\sqrt{7}$,
以O为原点,OA为x轴,OB为y轴,OS为z轴,建立空间直角坐标系,
则A(3$\sqrt{2}$,0,0),S(0,0,$\sqrt{7}$),E($\frac{3\sqrt{2}}{2}$,0,$\frac{\sqrt{7}}{2}$),D(0,-3$\sqrt{2}$,0),C(-3$\sqrt{2}$,0,0),
$\overrightarrow{DE}$=($\frac{3\sqrt{2}}{2}$,3$\sqrt{2}$,$\frac{\sqrt{7}}{2}$),$\overrightarrow{SC}$=(-3$\sqrt{2}$,0,$\sqrt{7}$),
设DE与SC所成角为θ,
则cosθ=$\frac{|\overrightarrow{DE}•\overrightarrow{SC}|}{|\overrightarrow{DE}|•|\overrightarrow{SC}|}$=$\frac{|\frac{25}{2}|}{\sqrt{\frac{97}{4}}•\sqrt{25}}$=$\frac{5}{\sqrt{97}}$,
sinθ=$\sqrt{1-\frac{25}{97}}$=$\frac{6\sqrt{2}}{\sqrt{97}}$,tanθ=$\frac{6\sqrt{2}}{5}$.
∴DE与SC所成角的正切值为$\frac{6\sqrt{2}}{5}$.
故答案为:$\frac{6\sqrt{2}}{5}$.
点评 本题考查异面直线所成角的正切值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1+2i | B. | 1+2i | C. | 1-2i | D. | -1-2i |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充要条件 | B. | 充分但不必要条件 | ||
| C. | 必要但不充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{13}{2}$ | C. | 12 | D. | 23 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com