练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    16．焦点是F（0，1）的抛物线的标准方程是（　　）
    A．x2=4yB．y2=4xC．x2=-4yD．y2=-4x

    分析 焦点是F（0，1）的抛物线满足的标准形式是x2=2py（p＞0），且$\frac{p}{2}=1$，由此能求出结果．

    解答 解：焦点是F（0，1）的抛物线的标准方程是x2=4y．
    故选：A．

    点评 本题考查抛物线的标准方程的求法，是基础题，解题时要认真审题，注意抛物线性质的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    6．已知数列{an}的前n项和为Sn，且${S_n}={n^2}-4n$，则a2-a1=2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．在△ABC中，角A，B，C所对应的边分别为a，b，c，若$\frac{sinA}{a}=\frac{\sqrt{3}cosC}{c}$，则∠C=60°．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．已知定义在R上的偶函数f（x），满足f（x+4）=f（x），f（x）=sinπx+2|sinπx|，x∈[0，2]，函数g（x）=f（x）-loga（x+$\frac{3}{2}$），若以g（x）=0在区间[-1，3]上至少6个根，则a的取值范围为（　　）
    A．[${4}^{\frac{1}{3}}$，+∞）B．[${4}^{\frac{1}{3}}$，6]C．[4，+∞）D．[3，4]

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

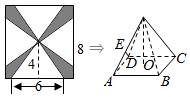    11．一块边长为8cm的正方形铁片按如图所示的阴影部分裁下，然后用余下的四个全等的等腰三角加工成一个正四棱锥（底面是正方形，从顶点向底面作垂线，垂足为底面中心的四棱锥）形容器，O为底面ABCD的中心，E为棱SA的中点，则DE与SC所成角的正切值为$\frac{6\sqrt{2}}{5}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

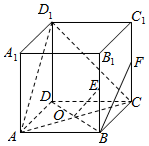    1．如图，在棱长为2的正方体ABCD-A1B1C1D1中，E、F分别是棱BB1、CC1的中点，AC与BD交于点O．
    （1）求证：OE⊥平面ACD1．
    （2）求异面直线OE与BF所成角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知数集M={a1，a2，…，an}（0≤a1＜a2＜…＜an，n≥2）具有性质P：对任意的i，j（1≤i≤j≤n），ai+aj与aj-ai两数中至少有一个属于M．
    （Ⅰ）分别判断数集{0，1，3}与{0，2，3，5}是否具有性质P，并说明理由；
    （Ⅱ）证明：a1=0，且an=$\frac{2}{n}（{a_1}+{a_2}+…+{a_{n-1}}+{a_n}）$；
    （Ⅲ）当n=5时，证明：a1，a2，a3，a4，a5成等差数列．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．记等差数列{an}的前n项和为Sn，若S3=2a3，S5=15，则a2016=2016．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．在函数y=xcosx，y=ex+x2，$y=lg\sqrt{{x^2}-2}$，y=xsinx偶函数的个数是（　　）
    A．3B．2C．1D．0

    查看答案和解析>>

    同步练习册答案