练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    1．已知x，y满足不等式$\left\{\begin{array}{l}x-4y≤-3\\ 3x+5y≤25\\ x≥1\end{array}\right.$，则函数z=2x+y取得最大值是（　　）
    A．3B．$\frac{13}{2}$C．12D．23

    分析 由约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合求出最值即可．

    解答 解：由约束条件作出可行域如图
    由图可知，使目标函数z=2x+y取得最大值时过点B，
    联立 $\left\{\begin{array}{l}{x-4y=-3}\\{3x+5y=25}\end{array}\right.$，解得 $\left\{\begin{array}{l}{x=5}\\{y=2}\end{array}\right.$，
    故z的最大值是：z=12，
    故选：C．

    点评 本题考查了简单的线性规划，考查了数形结合的解题思想方法，是中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

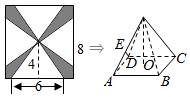    11．一块边长为8cm的正方形铁片按如图所示的阴影部分裁下，然后用余下的四个全等的等腰三角加工成一个正四棱锥（底面是正方形，从顶点向底面作垂线，垂足为底面中心的四棱锥）形容器，O为底面ABCD的中心，E为棱SA的中点，则DE与SC所成角的正切值为$\frac{6\sqrt{2}}{5}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．已知向量|$\overrightarrow{a}$|=1，|$\overrightarrow{b}$|=2，若|$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{3}$，则向量$\overrightarrow{a}$，$\overrightarrow{b}$的夹角为$\frac{π}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．不等式x2-2x+m＞0在R上恒成立的必要不充分条件是（　　）
    A．m＞2B．0＜m＜1C．m＞0D．m＞1

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．若直线a∥平面α，直线b在平面α内，则直线a与b的位置关系为（　　）
    A．一定平行B．一定异面
    C．一定相交D．可能平行、可能异面

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．在函数y=xcosx，y=ex+x2，$y=lg\sqrt{{x^2}-2}$，y=xsinx偶函数的个数是（　　）
    A．3B．2C．1D．0

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．复数Z满足（2+i）•Z=3-i，则|Z|等于（　　）
    A．1B．$\sqrt{2}$C．2D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

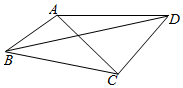    10．如图，在凸四边形ABCD中，AB=1，BC=$\sqrt{3}$，AC⊥CD，AC=CD，当∠ABC变化时，对角线BD的最大值为$\sqrt{6}$+1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

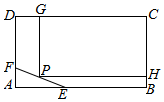    11．为了保护环境，实现城市绿化，某小区要在空地长方形ABCD上规划出一块长方形地面建造草坪CGPH，草坪一边落在CD上，一个顶点P在水池△AEF的边EF上，（如图，其中AB=200 m，BC=160m，AE=60m，AF=40m），设CG=xm，草坪的面积为f（x）．
    （1）求函数y=f（x）的解析式，并写出它的定义域；
    （2）求草坪面积的最大值，井求出此时CG的长度．（精确到整数）

    查看答案和解析>>

    同步练习册答案