
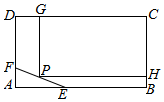
 为了保护环境,实现城市绿化,某小区要在空地长方形ABCD上规划出一块长方形地面建造草坪CGPH,草坪一边落在CD上,一个顶点P在水池△AEF的边EF上,(如图,其中AB=200 m,BC=160m,AE=60m,AF=40m),设CG=xm,草坪的面积为f(x).
为了保护环境,实现城市绿化,某小区要在空地长方形ABCD上规划出一块长方形地面建造草坪CGPH,草坪一边落在CD上,一个顶点P在水池△AEF的边EF上,(如图,其中AB=200 m,BC=160m,AE=60m,AF=40m),设CG=xm,草坪的面积为f(x).分析 根据CG=x,矩形CGPH面积为f(x),作EN⊥PH于点N,因为三角形AEF∽三角形PEN,得到对应边成比例得到EN,用160-EN得到HC,然后利用矩形的面积求法,长乘以宽得到y与x的函数关系式,最后利用基本不等式求出最大值即可.
解答 解:(1)如图示: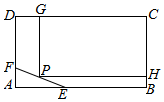
CG=x,矩形CGPH面积为f(x),
作EN⊥PH于点N,则 $\frac{EN}{40}$=$\frac{x-140}{60}$⇒EN=$\frac{2x-280}{3}$,
∴HC=160-$\frac{2x-280}{3}$=$\frac{760-2x}{3}$,
∴f(x)=x•$\frac{760-2x}{3}$=$\frac{1}{6}$•2x(760-2x),(140<x<200);
(2)由(1)得:f(x)=x•$\frac{760-2x}{3}$=$\frac{1}{6}$•2x(760-2x)≤$\frac{1}{2}$($\frac{760}{2}$)2=$\frac{72200}{3}$,
当2x=760-2x⇒x=190(m)即CG长为190m时,最大面积为 $\frac{72200}{3}$(m2).
点评 考查学生会根据实际问题选择合适的函数类型来解决实际问题,理解函数的最值及其几何意义.


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{13}{2}$ | C. | 12 | D. | 23 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{8}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $g(x)=\frac{3-2x}{x}$ | B. | $g(x)=\frac{2-x}{1+x}$ | C. | $g(x)=\frac{1-x}{2+x}$ | D. | $g(x)=\frac{3}{2+x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{\sqrt{15}}{3}$ | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{6}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com