
| A. | $g(x)=\frac{3-2x}{x}$ | B. | $g(x)=\frac{2-x}{1+x}$ | C. | $g(x)=\frac{1-x}{2+x}$ | D. | $g(x)=\frac{3}{2+x}$ |
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:解答题
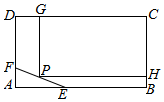 为了保护环境,实现城市绿化,某小区要在空地长方形ABCD上规划出一块长方形地面建造草坪CGPH,草坪一边落在CD上,一个顶点P在水池△AEF的边EF上,(如图,其中AB=200 m,BC=160m,AE=60m,AF=40m),设CG=xm,草坪的面积为f(x).
为了保护环境,实现城市绿化,某小区要在空地长方形ABCD上规划出一块长方形地面建造草坪CGPH,草坪一边落在CD上,一个顶点P在水池△AEF的边EF上,(如图,其中AB=200 m,BC=160m,AE=60m,AF=40m),设CG=xm,草坪的面积为f(x).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
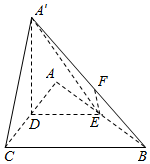 如图,△ABC是等腰直角三角形,∠ACB=90°,AC=2a,D,E分别为AC,AB的中点,沿DE将△ADE折起,得到如图所示的四棱锥A′-BCDE,F是A′B的中点.
如图,△ABC是等腰直角三角形,∠ACB=90°,AC=2a,D,E分别为AC,AB的中点,沿DE将△ADE折起,得到如图所示的四棱锥A′-BCDE,F是A′B的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | π | C. | $\frac{3π}{2}$ | D. | 2π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com