
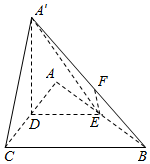
 如图,△ABC是等腰直角三角形,∠ACB=90°,AC=2a,D,E分别为AC,AB的中点,沿DE将△ADE折起,得到如图所示的四棱锥A′-BCDE,F是A′B的中点.
如图,△ABC是等腰直角三角形,∠ACB=90°,AC=2a,D,E分别为AC,AB的中点,沿DE将△ADE折起,得到如图所示的四棱锥A′-BCDE,F是A′B的中点.分析 (1)取A'C的中点G,连结DG、EF、GF.运用中位线定理证出四边形DEFG是平行四边形,从而得到EF∥DG,结合线面平行的判定定理,即可证出EF∥平面A'CD.
(2)在平面A′CD内作A'H⊥CD于点H,利用线面垂直的判定与性质,证出A'H⊥底面BCDE,从而得到点H和D重合时,四棱锥A'-BCDE体积取最大值.然后以DC、DE、DA'所在直线为x轴、y轴、z轴,建立空间直角坐标系利用向量法进行求解.
解答 解:(I)如图1,取A'C的中点G,连结DG、EF、GF,则
由中位线定理得DE∥BC、DE=$\frac{1}{2}$BC,且GF∥BC、GF=$\frac{1}{2}$BC.
∴DE∥GF且DE=GF,可得四边形DEFG是平行四边形,
∴EF∥DG
∵EF?平面A'CD,DG?平面A'CD,
∴EF∥平面A′CD.----(4分)
(II)在平面A′CD内作A'H⊥CD于点H,
∵DE⊥A'D,DE⊥CD,且A'D∩CD=D
∴DE⊥平面A'CD,可得A'H⊥DE,
又∵DE∩CD=D,∴A'H⊥底面BCDE,即A'H就是四棱锥A'-BCDE的高.
由A'H≤AD,得点H和D重合时,四棱锥A'-BCDE体积取最大值.--(8分)
分别以DC、DE、DA'所在直线为x轴、y轴、z轴,建立空间直角坐标系如,2,
则A'(0,0,a),B(a,2a,0),E(0,a,0),
∴$\overrightarrow{A′B}$=(a,2a,-a),$\overrightarrow{A′E}$=(0,a,-a),
设平面A'BE的一个法向量为$\overrightarrow{m}$=(x,y,z),
由$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{A′B}=ax+2ay-az=0}\\{\overrightarrow{m}•\overrightarrow{A′E}=ay-az=0}\end{array}\right.$得$\left\{\begin{array}{l}{x+2y-z=0}\\{y=z}\end{array}\right.$
取y=1,得x=-1,z=1.得到$\overrightarrow{m}$=(-,1,1),
同理,可求得平面A'CD的一个法向量$\overrightarrow{n}$=(0,1,0)
∴cos$<\overrightarrow{m},\overrightarrow{n}>$=$\frac{\overrightarrow{m}•\overrightarrow{n}}{\overrightarrow{|m|}•\overrightarrow{|n|}}$=$\frac{-1×0+1×1+1×0}{\sqrt{3}×1}$=$\frac{\sqrt{3}}{3}$
故平面A'CD与平面A'BE夹角的余弦值为$\frac{\sqrt{3}}{3}$
综上所述,四棱锥A'-BCDE体积取最大值时,平面A′CD与平面A′BE夹角的余弦值等于$\frac{\sqrt{3}}{3}$----(12分)
点评 本题给出平面图形的折叠,求证线面平行并求四棱锥A'-BCDE体积取最大值时,平面A′CD与平面A′BE夹角的余弦值.着重考查了三角形中位线定理、线面平行的判定定理和利用空间向量的方法研究平面与平面所成角等知识,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 甲模型拟合效果最好 | B. | 乙模型拟合效果最好 | ||
| C. | 丙模型拟合效果最好 | D. | 拟合效果与R2的值无关 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{8}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $g(x)=\frac{3-2x}{x}$ | B. | $g(x)=\frac{2-x}{1+x}$ | C. | $g(x)=\frac{1-x}{2+x}$ | D. | $g(x)=\frac{3}{2+x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$a | B. | $\frac{\sqrt{3}}{2}$a | C. | $\frac{\sqrt{6}}{3}$a | D. | $\frac{\sqrt{6}}{6}$a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-3] | B. | [-4,1) | C. | (-3,1) | D. | (-∞,-3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com