
分析 (I)先求出f′(1)=0,f(x)=$\frac{1+2lnx}{{x}^{2}}$,再求函数f(x)在点(1,f(1))处的切线方程;
(Ⅱ)由题意,a=$\frac{1+2lnx}{{x}^{2}}$=f(x),确定函数f(x)在[$\frac{1}{e}$,1)上单调递增,在(1,e]上单调递减,即可求实数a的取值范围;
(Ⅲ)构造函数g(x)=f(x)-klnx=$\frac{1+2lnx}{{x}^{2}}$-klnx,若函数g(x)在(0,+∞)上单调递增,则g′(x)=-$\frac{4lnx}{{x}^{3}}$-$\frac{k}{x}$≥0,求出k的范围,再利用其反面,即可求实数k的取值范围.
解答 解:(I)∵f(x)=$\frac{1+2lnx}{{x}^{2}}$+2f′(1)x,
∴f′(x)=-$\frac{4lnx}{{x}^{3}}$+2f′(1),
∴f′(1)=2f′(1),
∴f′(1)=0,f(x)=$\frac{1+2lnx}{{x}^{2}}$,
∴f(1)=1,
∴函数f(x)在点(1,f(1))处的切线方程是y-1=0;
(Ⅱ)由题意,a=$\frac{1+2lnx}{{x}^{2}}$=f(x),
∴f′(x)=-$\frac{4lnx}{{x}^{3}}$=0,可得x=1.
∴函数f(x)在[$\frac{1}{e}$,1)上单调递增,在(1,e]上单调递减,
∵f($\frac{1}{e}$)=-e2,f(1)=1,f(e)=$\frac{3}{{e}^{2}}$,关于x的方程f(x)=a+2f′(1)x在[$\frac{1}{e}$,e]上有两个不同的实数根,
∴$\frac{3}{{e}^{2}}$<a<1;
(Ⅲ)构造函数g(x)=f(x)-klnx=$\frac{1+2lnx}{{x}^{2}}$-klnx,
∴g′(x)=-$\frac{4lnx}{{x}^{3}}$-$\frac{k}{x}$,
若函数g(x)在(0,+∞)上单调递增,则g′(x)=-$\frac{4lnx}{{x}^{3}}$-$\frac{k}{x}$≥0,
∴k≤-$\frac{4lnx}{{x}^{2}}$,
令h(x)=-$\frac{4lnx}{{x}^{2}}$,则h′(x)=-$\frac{4x-8xlnx}{{x}^{4}}$,
∴函数h(x)在(0,$\sqrt{e}$)上单调递减,($\sqrt{e}$,+∞)上单调递增,
∴x=$\sqrt{e}$时,h(x)min=-$\frac{2}{e}$,
∴k≤-$\frac{2}{e}$,
∵存在x1>x2>0,使f(x1)-klnx1≤f(x2)-klnx2成立,
∴k>-$\frac{2}{e}$.
点评 本题考查导数知识的综合运用,考查导数的几何意义,考查函数的单调性,考查学生分析解决问题的能力,属于中档题.


 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:解答题
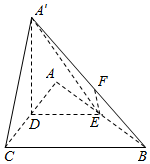 如图,△ABC是等腰直角三角形,∠ACB=90°,AC=2a,D,E分别为AC,AB的中点,沿DE将△ADE折起,得到如图所示的四棱锥A′-BCDE,F是A′B的中点.
如图,△ABC是等腰直角三角形,∠ACB=90°,AC=2a,D,E分别为AC,AB的中点,沿DE将△ADE折起,得到如图所示的四棱锥A′-BCDE,F是A′B的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 1 | C. | 2 | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | π | C. | $\frac{3π}{2}$ | D. | 2π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 31 | B. | 5 | C. | $\frac{31}{16}$ | D. | $\frac{15}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com