
分析 (1)由x∈[-$\frac{π}{2}$,π]和不等式的性质可得$\frac{1}{2}$x+$\frac{π}{4}$∈[0,$\frac{3π}{4}$],再由余弦函数可得值域;
(2)由题意结合函数图象可得ω范围,再由对称性可得$\frac{7π}{12}$为函数过最低点的一条对称轴,可得ω方程,综合可得ω值;
(3)由(1)可得f(x2)∈[-$\sqrt{2}$,2],题目转化为当x1∈[0,α]时,g(x1)=2sin(2x1+$\frac{π}{3}$)的值域是[-$\sqrt{2}$,2]的子集,由正弦函数的图象可得$\frac{π}{3}$<2α+$\frac{π}{3}$≤$\frac{5π}{4}$,解不等式可得.
解答 解:(1)当x∈[-$\frac{π}{2}$,π]时,$\frac{1}{2}$x∈[-$\frac{π}{4}$,$\frac{π}{2}$],
∴$\frac{1}{2}$x+$\frac{π}{4}$∈[0,$\frac{3π}{4}$],∴cos($\frac{1}{2}$x+$\frac{π}{4}$)∈[-$\frac{\sqrt{2}}{2}$,1],
∴2cos($\frac{1}{2}$x+$\frac{π}{4}$)∈[-$\sqrt{2}$,2],
∴f(x)在[-$\frac{π}{2}$,π]上的值域为:[-$\sqrt{2}$,2];
(2)∵g($\frac{π}{3}$)=g($\frac{5}{6}$π),且g(x)在($\frac{π}{3}$,$\frac{5}{6}$π)内有最小值,无最大值,
∴$\frac{5}{6}$π-$\frac{π}{3}$<$\frac{2π}{ω}$,解得ω<4,又由对称性可得$\frac{1}{2}$($\frac{π}{3}$+$\frac{5}{6}$π)=$\frac{7π}{12}$为函数过最低点的一条对称轴,
∴ω•$\frac{7π}{12}$+$\frac{π}{3}$=2kπ-$\frac{π}{2}$,解得ω=$\frac{24k}{7}$-$\frac{10}{7}$,k∈Z,
结合0<ω<4可得当且仅当k=1时,ω=2符合题意;
(3)由(1)可得当x2∈[-$\frac{π}{2}$,π],f(x2)∈[-$\sqrt{2}$,2],
由(2)知g(x)=2sin(2x+$\frac{π}{3}$),
∵对任意x1∈[0,α],都存在x2∈[-$\frac{π}{2}$,π],使得f(x2)=g(x1),
∴当x1∈[0,α]时,g(x1)=2sin(2x1+$\frac{π}{3}$)的值域是[-$\sqrt{2}$,2]的子集,
∴sin(2x1+$\frac{π}{3}$)的值域是[-$\frac{\sqrt{2}}{2}$,1]的子集,
∵x1∈[0,α],∴2x1+$\frac{π}{3}$∈[$\frac{π}{3}$,2α+$\frac{π}{3}$],
结合正弦函数的图象可得$\frac{π}{3}$<2α+$\frac{π}{3}$≤$\frac{5π}{4}$,
解得0<α≤$\frac{11π}{12}$,故α的取值范围为(0,$\frac{11π}{12}$]
点评 本题考查三角函数的图象和性质,涉及三角函数对称性和集合间的包含关系以及数形结合的思想,属中档题.


科目:高中数学 来源: 题型:填空题
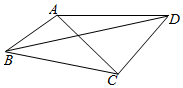 如图,在凸四边形ABCD中,AB=1,BC=$\sqrt{3}$,AC⊥CD,AC=CD,当∠ABC变化时,对角线BD的最大值为$\sqrt{6}$+1.
如图,在凸四边形ABCD中,AB=1,BC=$\sqrt{3}$,AC⊥CD,AC=CD,当∠ABC变化时,对角线BD的最大值为$\sqrt{6}$+1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
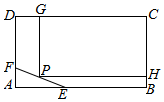 为了保护环境,实现城市绿化,某小区要在空地长方形ABCD上规划出一块长方形地面建造草坪CGPH,草坪一边落在CD上,一个顶点P在水池△AEF的边EF上,(如图,其中AB=200 m,BC=160m,AE=60m,AF=40m),设CG=xm,草坪的面积为f(x).
为了保护环境,实现城市绿化,某小区要在空地长方形ABCD上规划出一块长方形地面建造草坪CGPH,草坪一边落在CD上,一个顶点P在水池△AEF的边EF上,(如图,其中AB=200 m,BC=160m,AE=60m,AF=40m),设CG=xm,草坪的面积为f(x).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
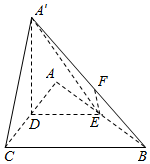 如图,△ABC是等腰直角三角形,∠ACB=90°,AC=2a,D,E分别为AC,AB的中点,沿DE将△ADE折起,得到如图所示的四棱锥A′-BCDE,F是A′B的中点.
如图,△ABC是等腰直角三角形,∠ACB=90°,AC=2a,D,E分别为AC,AB的中点,沿DE将△ADE折起,得到如图所示的四棱锥A′-BCDE,F是A′B的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com